/Szkoła średnia/Nierówności/Liniowe/Z parametrem

Zadanie nr 6313475

Dodaj do ulubionych
Dodaj do rozwiązanych

Znajdź te wartości parametru 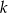k , dla których zbiorem rozwiązań nierówności 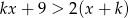kx + 9 > 2(x + k) jest przedział (− ∞ ;3) .

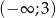Rozwiązanie

Przekształćmy podaną nierówność

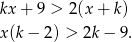
kx + 9 > 2(x + k) x(k − 2) > 2k − 9.

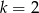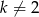Jeżeli k = 2 , to nierówność jest zawsze spełniona (dla dowolnego x ), możemy zatem założyć, że k ⁄= 2 . Chcielibyśmy podzielić obie strony nierówności przez 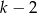k− 2 , ale żeby to zrobić, musimy wiedzieć jaki jest znak tego wyrażenia. Jeżeli 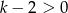k− 2 > 0 , to otrzymaną nierówność możemy zapisać w postaci

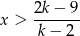
x > 2k-−-9- k− 2

i widać, że jej rozwiązaniem nie może być przedział 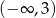(− ∞ ,3) (bo spełniają ją duże liczby, a nie małe).

Zatem 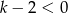k− 2 < 0 i mamy nierówność

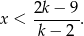
2k−--9- x < k − 2 .

Jeżeli jej zbiorem rozwiązań ma być przedział 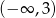(− ∞ ,3) , to musimy mieć

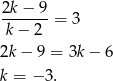
2k − 9 -------= 3 k − 2 2k − 9 = 3k− 6 k = − 3 .

 
Odpowiedź: k = − 3

Wersja PDF