/Szkoła średnia/Prawdopodobieństwo/Z definicji/Proces technologiczny

Zadanie nr 5499496

W pojemniku znajduje się 200 wybrakowanych części. 60 sztuk odrzucono z powodu wystąpienia wady 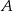A , 40 sztuk z powodu wady 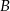B , pozostałe z powodu wady 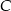C . Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie dwie części z wadą B .

Wersja PDF

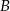Rozwiązanie

Ustalmy, że zdarzenia elementarne to nieuporządkowane trójki 3 części. Mamy zatem

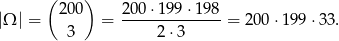
( ) |Ω | = 200 = 2-00⋅-199⋅-198 = 2 00⋅1 99⋅3 3. 3 2 ⋅3

Musimy wybrać dwie części z wadą 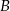B i trzecią z inną wadą (tu jest ważne, że mają być dokładnie dwie części z wadą 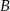B , czyli trzecia nie jest 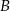B ), zatem zdarzeń sprzyjających jest

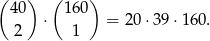
( ) ( ) 40 1 60 ⋅ = 20 ⋅39⋅ 160. 2 1

Stąd

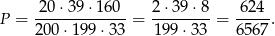
20⋅3 9⋅1 60 2 ⋅39⋅ 8 624 P = -------------= -------- = -----. 200 ⋅199 ⋅33 19 9⋅33 6 567

 
Odpowiedź: -624 6567

Wersja PDF