/Szkoła średnia/Prawdopodobieństwo/Z definicji/Proces technologiczny

Zadanie nr 6993965

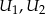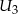W fabryce zainstalowano 3 urządzenia U 1,U2 i U 3 niezależnie wykrywające awarie. Prawdopodobieństwo wykrycia awarii przez kolejne urządzenia wynoszą 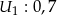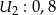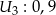U 1 : 0 ,7 , U 2 : 0,8 , U 3 : 0,9 . Oblicz prawdopodobieństwo wykrycia awarii przez:

  • dokładnie 2 urządzenia,
  • co najmniej 1 urządzenie.
Wersja PDF

Rozwiązanie

  • Opisane zdarzenie to
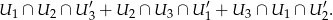
    ′ ′ ′ U1 ∩ U 2 ∩ U 3 + U2 ∩ U 3 ∩ U 1 + U3 ∩ U 1 ∩ U 2.

    (dwa z urządzeń mają wykryć awarię a trzecie nie). Z niezależności zdarzeń mamy

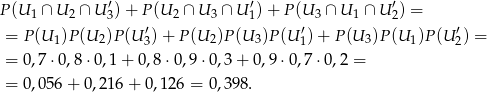
    P (U ∩ U ∩ U ′)+ P(U ∩ U ∩ U′) + P (U ∩ U ∩ U ′) = 1 2 3 2 3 1 3 1 2 = P (U 1)P(U 2)P(U ′3)+ P(U 2)P(U 3)P(U ′1) + P(U 3)P (U1)P (U2′) = = 0 ,7 ⋅0,8 ⋅0,1 + 0,8 ⋅0,9 ⋅0,3+ 0,9 ⋅0,7⋅ 0,2 = = 0 ,0 56+ 0,216 + 0,126 = 0,398.

     
    Odpowiedź: 0,398

  • Intersujące nas zdarzenie to
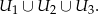
    U ∪ U ∪ U . 1 2 3

    Sposób I

    Liczymy (korzystamy z łatwego do wyprowadzenia wzoru na prawdopodobieństwo sumy i z niezależności zdarzeń)

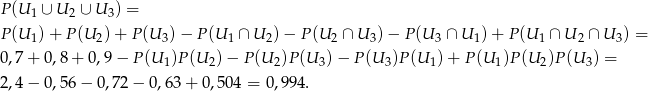
    P (U 1 ∪ U 2 ∪ U 3) = P (U )+ P (U )+ P (U ) − P (U ∩ U )− P (U ∩ U )− P(U ∩ U )+ P(U ∩ U ∩ U ) = 1 2 3 1 2 2 3 3 1 1 2 3 0 ,7+ 0 ,8+ 0 ,9− P(U 1)P(U 2)− P(U 2)P(U 3)− P(U 3)P(U 1)+ P(U 1)P(U 2)P (U3) = 2 ,4− 0 ,56− 0,72− 0,63 + 0,504 = 0,994.

    Sposób II

    Rachunki będą znacznie prostsze jeżeli policzymy prawdopodobieństwo zdarzenia przeciwnego.

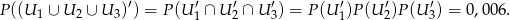
    P((U ∪ U ∪ U )′) = P(U ′ ∩ U ′∩ U ′) = P(U ′)P(U ′)P (U′) = 0 ,006. 1 2 3 1 2 3 1 2 3

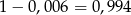    Szukane prawdopodobieństwo wynosi zatem 1 − 0,006 = 0,994 .  
    Odpowiedź: 0,994

Wersja PDF