Zadanie nr 1927860
Rozwiąż równanie 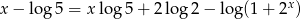 .
.
Rozwiązanie
Przekształcamy podane równanie.
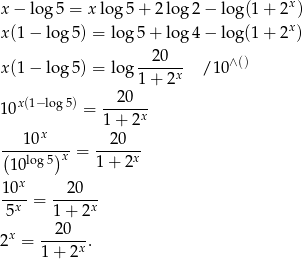
Podstawmy teraz 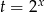 .
.
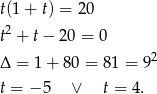
Ujemne rozwiązanie odrzucamy i mamy
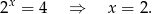
Odpowiedź: 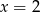
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 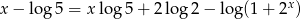 .
.
Przekształcamy podane równanie.
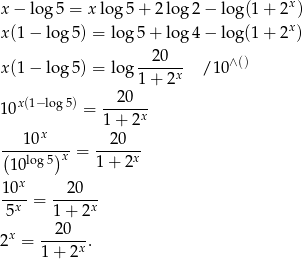
Podstawmy teraz 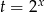 .
.
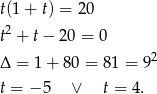
Ujemne rozwiązanie odrzucamy i mamy
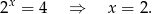
Odpowiedź: