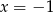Zadanie nr 6714892
Wyznacz miejsca zerowe funkcji 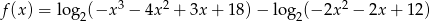 .
.
Rozwiązanie
Sposób I
Powinniśmy rozpocząć od wyznaczenia dziedziny funkcji, ale zostawimy to sobie na koniec – po prostu sprawdzimy otrzymane rozwiązanie.
Rozwiązujemy równanie (korzystamy z różnowartościowości logarytmu)
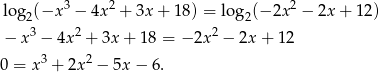
Szukamy teraz miejsc zerowych prawej strony – łatwo zauważyć, że jednym z nich jest 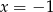 . Dzielimy teraz ten wielomian przez
. Dzielimy teraz ten wielomian przez 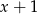 . My jak zwykle zrobimy to grupując wyrazy.
. My jak zwykle zrobimy to grupując wyrazy.
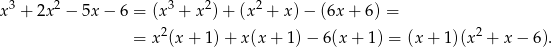
Zauważmy teraz, że miejsca zerowe wielomianu w nawiasie (czyli 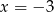 i
i 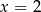 ) są dokładnie takie same jak miejsca zerowe wielomianu w drugim z logarytmów
) są dokładnie takie same jak miejsca zerowe wielomianu w drugim z logarytmów
![[ ] log2(− 2x2 − 2x + 1 2) = log2 −2 (x2 + x− 6) ,](https://img.zadania.info/zad/6714892/HzadR6x.gif)
w takim razie liczby te nie należą do dziedziny równania. Z drugiej strony, łatwo sprawdzić, że dla 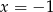 mamy
mamy
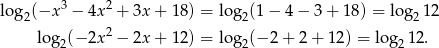
Jedynym miejscem zerowym funkcji 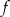 jest więc
jest więc 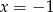 .
.
Sposób II
Tym razem postępujmy bardziej szkolnie i rozpocznijmy od wyznaczenia dziedziny równania.
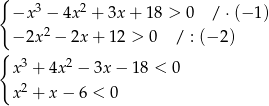
Rozwiążmy najpierw drugą nierówność
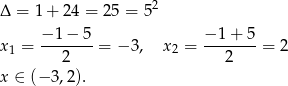
Teraz zajmijmy się wielomianem stopnia 3 – łatwo zauważyć, że jednym z jego pierwiastków jest 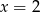 . Dzielimy teraz ten wielomian przez
. Dzielimy teraz ten wielomian przez 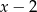 . My jak zwykle zrobimy to grupując wyrazy.
. My jak zwykle zrobimy to grupując wyrazy.
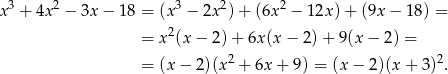
To oznacza, że rozwiązaniem pierwszej nierówności jest zbiór
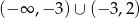
i dziedziną funkcji  jest przedział
jest przedział 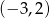 . Powyższe rozkłady pozwalają nam też bardzo uprościć wzór funkcji
. Powyższe rozkłady pozwalają nam też bardzo uprościć wzór funkcji 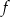
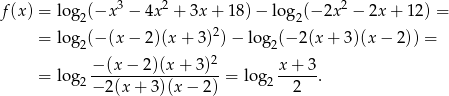
Pozostało rozwiązać równanie
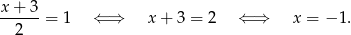
Liczba ta oczywiście należy do dziedziny równania.
Odpowiedź: