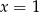Zadanie nr 8382688
Rozwiąż równanie ![1 log4(1 + log3[1 + log2(x + 3)]) = 2](https://img.zadania.info/zad/8382688/HzadT0x.gif) .
.
Rozwiązanie
Liczymy
![1 lo g4(1+ lo g3[1+ log 2(x+ 3)]) = lo g44 2 lo g (1+ lo g [1+ log (x+ 3)]) = lo g 2 4 3 2 4 1 + log3[1 + log2(x + 3)] = 2 lo g3[1+ log 2(x+ 3)] = 1 lo g3[1+ log 2(x+ 3)] = lo g33 1 + log2(x + 3 ) = 3 lo g (x + 3) = 2 2 lo g2(x + 3) = log2 22 x + 3 = 4 ⇒ x = 1 .](https://img.zadania.info/zad/8382688/HzadR0x.gif)
Na koniec wypada sprawdzić, czy 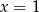 jest rzeczywiście rozwiązaniem (tzn. czy należy do dziedziny równania), to jednak jest łatwe:
jest rzeczywiście rozwiązaniem (tzn. czy należy do dziedziny równania), to jednak jest łatwe:
![log (1 + log [1 + log (1 + 3)]) = log (1 + log (1 + 2)) = lo g 2 = 1. 4 3 2 4 3 4 2](https://img.zadania.info/zad/8382688/HzadR2x.gif)
Odpowiedź: 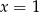
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie ![1 log4(1 + log3[1 + log2(x + 3)]) = 2](https://img.zadania.info/zad/8382688/HzadT0x.gif) .
.
Liczymy
![1 lo g4(1+ lo g3[1+ log 2(x+ 3)]) = lo g44 2 lo g (1+ lo g [1+ log (x+ 3)]) = lo g 2 4 3 2 4 1 + log3[1 + log2(x + 3)] = 2 lo g3[1+ log 2(x+ 3)] = 1 lo g3[1+ log 2(x+ 3)] = lo g33 1 + log2(x + 3 ) = 3 lo g (x + 3) = 2 2 lo g2(x + 3) = log2 22 x + 3 = 4 ⇒ x = 1 .](https://img.zadania.info/zad/8382688/HzadR0x.gif)
Na koniec wypada sprawdzić, czy 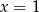 jest rzeczywiście rozwiązaniem (tzn. czy należy do dziedziny równania), to jednak jest łatwe:
jest rzeczywiście rozwiązaniem (tzn. czy należy do dziedziny równania), to jednak jest łatwe:
![log (1 + log [1 + log (1 + 3)]) = log (1 + log (1 + 2)) = lo g 2 = 1. 4 3 2 4 3 4 2](https://img.zadania.info/zad/8382688/HzadR2x.gif)
Odpowiedź: