Zadania.info
Największy internetowy zbiór zadań z matematyki
cornersUpL
cornersUpR

Zadania

Na skróty

Recenzje

Linki sponsorowane

cornersM
Zaloguj się

Linki sponsorowane

cornersR
Zadanie nr 1204933

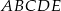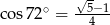
Dany jest pięciokąt foremny ABCDE o boku długości a . Wiedząc, że √- cos72 ∘ = -5−-1 4

  • wykaż, że długość przekątnej pięciokąta 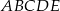ABCDE jest równa √ - 1+2-5a ;
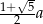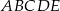  • oblicz długość promienia okręgu wpisanego w pięciokąt ABCDE .
Wersja PDF
Rozwiązanie

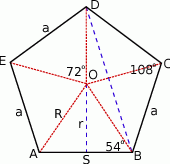
Zaczynamy od rysunku i od razu zauważmy, że 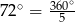∘ 360∘ 72 = 5 to dokładnie miara kąta środkowego ∡AOB .

PIC

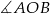  • Ponieważ
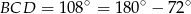
    BCD = 108∘ = 180 ∘ − 7 2∘

    to długość przekątnej 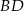BD możemy wyliczyć z twierdzenia cosinusów zastosowanego do trójkąta BCD .

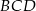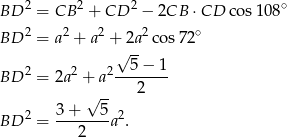
    BD 2 = CB 2 + CD 2 − 2CB ⋅CD cos 108∘ 2 2 2 2 ∘ BD = a + a + 2a cos72 √ -- BD 2 = 2a 2 + a2--5−--1- √ -- 2 2 3+ 5 2 BD = -------a . 2

    Pozostało sprawdzić, czy liczba ta zgadza się z podaną wartością – liczymy jej kwadrat.

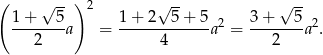
    ( √ -- ) 2 √ -- √ -- 1-+---5-a = 1-+-2--5-+-5a 2 = 3+----5a2. 2 4 2

    Obie liczby są więc równe.

  • Odległość, którą mamy wyliczyć to odległość środka pieciokąta od jego boku. Można to zrobić na wiele różnych sposobów, my pokażemy trzy z nich.

    Sposób I

    Długość odcinka 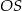OS możemy wyliczyć z trójkąta prostokątnego 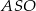ASO , musimy jednak najpierw wyliczyć długość odcinka 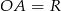OA = R (do niczego nam to niepotrzebne, ale jest to promień okręgu opisanego na pięciokącie). Długość tego odcinka wyliczamy z twierdzenia cosinusów zastosowanego do trójkąta ABO

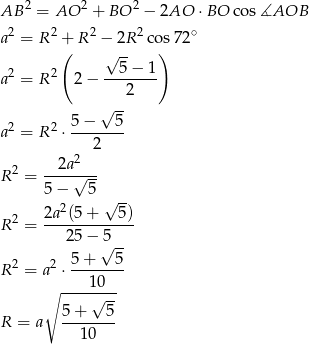
    AB 2 = AO 2 + BO 2 − 2AO ⋅ BO co s∡AOB 2 2 2 2 ∘ a = R + R − 2R cos72 ( √ -- ) a 2 = R2 2 − --5−--1- 2 √ -- a 2 = R2 ⋅ 5-−--5- 2 2a 2 R 2 = ----√--- 5 − 5 √ -- 2a 2(5+ 5) R 2 = ------------- 2 5− √5-- 2 2 5-+---5- R = a ⋅ 1 0 ∘ ----√--- 5+ 5 R = a --10----

    Liczymy teraz szukaną długość odcinka OS

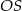
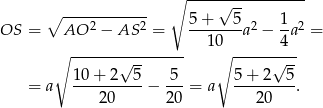
    ∘ ----------------- ∘ ------------ 5 + √ 5- 1 OS = AO 2 − AS 2 = --------a2 − -a2 = ∘ ---------------- 10∘ -------4- √ -- √ -- = a 1-0+-2---5− -5-= a 5-+-2---5. 20 20 2 0

    Sposób II

    Podobnie jak poprzednio patrzymy na trójkąt prostokątny 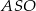ASO , ale tym razem wyliczymy tangens kąta 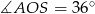∡AOS = 36∘ . Aby to zrobić korzystamy ze wzorów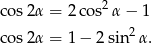

    2 co s2α = 2cos α− 1 co s2α = 1− 2 sin2α .

    Z tych wzorów mamy

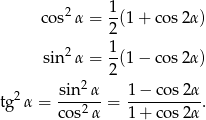
    cos2 α = 1-(1+ cos2α ) 2 2 1 sin α = 2-(1− cos2α ) 2 tg2 α = -sin--α = 1-−-cos2-α. co s2α 1 + cos2 α

    Stąd

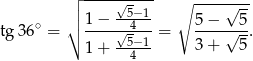
    ---------- ┌│ √ 5− 1 ∘ ----√--- ∘ │∘ 1−----4--- 5-−---5- tg 36 = √-5−-1 = 3 + √ 5. 1+ 4

    I dalej

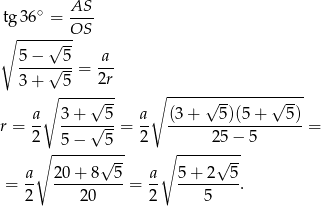
    AS tg3 6∘ = ---- ∘ -------OS 5 − √ 5 a ----√---= --- 3 + 5 2r ∘ ----√--- ∘ ------√--------√--- a- 3+--√-5- a- (3+----5)(5+----5)- r = 2 5− 5 = 2 25− 5 = ∘ ------√--- ∘ -----√--- a 20 + 8 5 a 5 + 2 5 = -- ----------= -- --------. 2 20 2 5

    Sposób III

    Tym razem rozpatrzmy trójkąt równoramienny 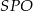SP O , gdzie 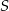S i P to środki kolejnych boków pięciokąta.

    PIC

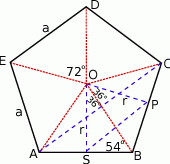
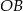    Dwa z jego boków są równe promieniowi r okręgu wpisanego w pięciokąt, a trzeci bok ma długość równą połowie przekątnej. Ponieważ prosta OB zawiera wysokość tego trójkąta, mamy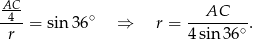

    -A4C- ∘ --AC----- r = sin 36 ⇒ r = 4 sin 36∘.

    Długość przekątnej 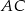AC wyliczyliśmy w poprzednim punkcie, pozostało więc wyliczyć 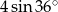∘ 4 sin 36 . Zrobimy to korzystając ze wzoru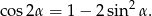

    cos 2α = 1 − 2 sin 2α.

    Dla 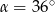∘ α = 36 mamy

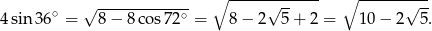
    √ ------------- ∘ -----√------- ∘ ------√--- 4 sin 36∘ = 8 − 8 cos 72∘ = 8 − 2 5 + 2 = 10 − 2 5 .

    Stąd mamy

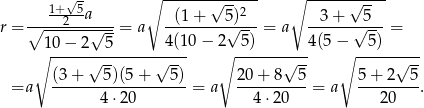
    √- ∘ ------√------ ∘ ------√---- 1+--5a (1 + 5)2 3 + 5 r = ∘---2---√---= a --------√---- = a ------√----= ∘ 10−--2--5-------4(10 − 2∘ -5)-------4(5−∘ --5)----- √ -- √ -- √ -- √ -- =a (3+----5)(5+----5)-= a 20-+-8--5-= a 5-+-2---5. 4 ⋅20 4 ⋅20 2 0

     
    Odpowiedź: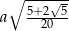 ∘ ----√- a 5+220-5

    Dla ciekawskich.
    Ponieważ pole pięciokąta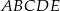 ABCDE jest równe 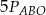5PABO , więc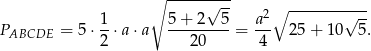

    ∘ --------- √ -- 2∘ -------√--- P = 5 ⋅ 1-⋅a⋅ a 5-+-2--5-= a-- 25 + 10 5. ABCDE 2 20 4

    Liczba 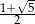- 1+√-5 2 , która pojawiła się w treści zadania to tak zwana złota liczba, ma ona wiele interesujących własności. Polecam wygooglać sobie ’pięciokąt foremy’, ’złoty podział’ lub ’golden ratio’.

Wersja PDF
Twoje uwagi
Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!