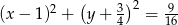Zadanie nr 7309775
Wyznacz równanie okręgu stycznego wewnętrznie do okręgu o równaniu 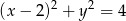 i do prostej
i do prostej 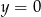 , którego środek ma współrzędne różnych znaków i leży na wykresie funkcji
, którego środek ma współrzędne różnych znaków i leży na wykresie funkcji 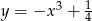 .
.
Rozwiązanie
Dany okrąg to oczywiście okrąg o środku 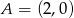 i promieniu
i promieniu 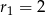 . Szkicujemy tę sytuację.
. Szkicujemy tę sytuację.
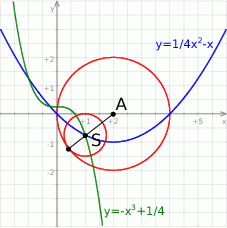
Z rysunku powinno być jasne, że środek 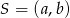 każdego okręgu wewnętrznie stycznego do danego okręgu i do prostej
każdego okręgu wewnętrznie stycznego do danego okręgu i do prostej 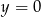 ma pierwszą współrzędną dodatnią, więc możemy założyć, że
ma pierwszą współrzędną dodatnią, więc możemy założyć, że 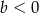 (bo z założenia współrzędne punktu
(bo z założenia współrzędne punktu 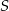 mają być różnych znaków). Styczność do osi
mają być różnych znaków). Styczność do osi 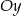 oznacza, że promień
oznacza, że promień 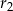 szukanego okręgu jest równy
szukanego okręgu jest równy 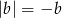 . Szukamy więc okręgu postaci
. Szukamy więc okręgu postaci
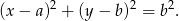
Teraz spróbujmy rozszyfrować styczność wewnętrzną szukanego i danego okręgu. Dwa okręgi są styczne wewnętrznie, gdy różnica długości ich promieni jest równa odległości ich środków. Mamy zatem
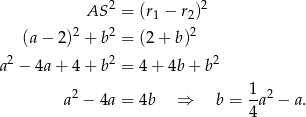
Teraz pozostało wykorzystać informację o tym, że punkt 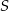 leży na wykresie funkcji
leży na wykresie funkcji 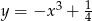 . Otrzymujemy stąd
. Otrzymujemy stąd 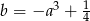 , co prowadzi do równania
, co prowadzi do równania
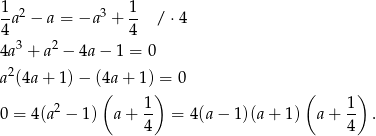
Ponieważ interesują nas tylko dodatnie wartości  , mamy stąd
, mamy stąd 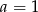 . Zatem
. Zatem 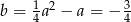 ,
, 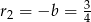 i szukany okrąg ma równanie
i szukany okrąg ma równanie
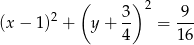
Odpowiedź: