Zadanie nr 9473027
Dane są okręgi o równaniach 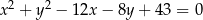 i
i 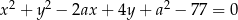 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru  , dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
, dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
Rozwiązanie
Zapiszmy równania danych okręgów tak, aby było widać jakie są ich środki i promienie.
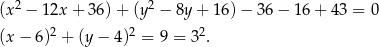
Zatem pierwszy okrąg ma środek 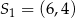 i promień
i promień 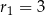 .
.
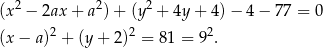
Zatem drugi okrąg ma środek 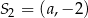 i promień
i promień 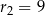 .
.
Jeżeli okręgi mają mieć jeden punkt wspólny, to muszą być styczne, czyli odległość ich środków musi być równa sumie lub różnicy ich promieni (w zależności od tego, czy styczność ma być zewnętrzna, czy wewnętrzna).
W pierwszym przypadku mamy równanie
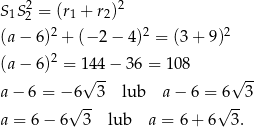
W drugim przypadku mamy
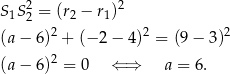
Na koniec rysunek całej sytuacji.
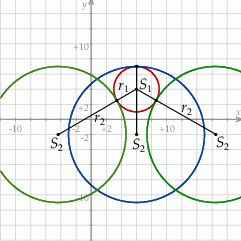
Odpowiedź: