Zadanie nr 2292510
Prosta przechodząca przez wierzchołek 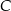 kwadratu
kwadratu 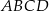 przecina przedłużenia jego boków
przecina przedłużenia jego boków 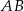 i
i 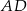 odpowiednio w punktach
odpowiednio w punktach 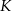 i
i 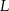 (zobacz rysunek).
(zobacz rysunek).
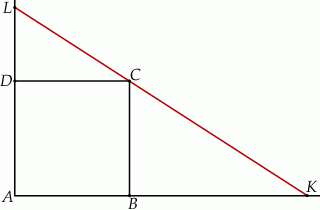
Wykaż, że
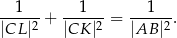
Rozwiązanie
Oznaczmy 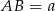 i
i 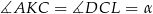 .
.
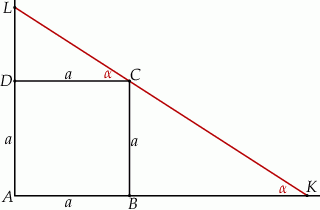
W trójkątach prostokątnych 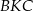 i
i 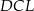 mamy
mamy
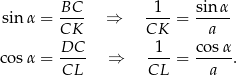
Stąd
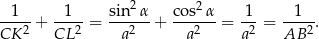
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Prosta przechodząca przez wierzchołek 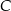 kwadratu
kwadratu 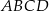 przecina przedłużenia jego boków
przecina przedłużenia jego boków 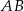 i
i 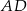 odpowiednio w punktach
odpowiednio w punktach 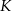 i
i 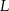 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że
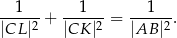
Oznaczmy 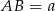 i
i 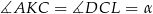 .
.

W trójkątach prostokątnych 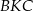 i
i 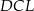 mamy
mamy
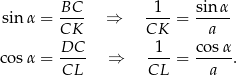
Stąd