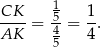/Szkoła średnia/Geometria/Planimetria/Czworokąt/Kwadrat

Zadanie nr 7937456

Dodaj do ulubionych
Dodaj do rozwiązanych

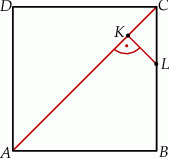
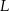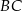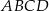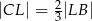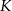Punkt L leży na boku BC kwadratu ABCD oraz 2 |CL | = 3|LB | . Punkt K leży na przekątnej 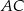AC i odcinek 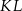KL jest prostopadły do 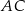AC (zobacz rysunek).

PIC

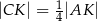Wykaż, że |CK | = 14|AK | .

Rozwiązanie

Dana równość 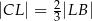2 |CL | = 3|LB | oznacza, że

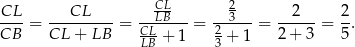
CL- 2 CL--= ---CL---- = --LB---= --3---= --2---= 2. CB CL + LB CLLB-+ 1 23 + 1 2+ 3 5

Sposób I

Trójkąt 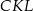CKL jest równoramiennym trójkątem prostokątnym (połówka kwadratu), więc

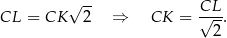
CL = CK √ 2- ⇒ CK = C√L-. 2

Ponadto, 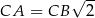√ -- CA = CB 2 , więc

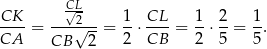
CK C√L- 1 CL 1 2 1 ----= ---2√---= -⋅ ----= -⋅ --= -. CA CB 2 2 CB 2 5 5

To oznacza, że 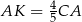AK = 45CA i

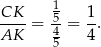
1 CK--= 5-= 1. AK 45 4

Sposób II

Jeżeli oznaczymy 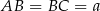AB = BC = a , to

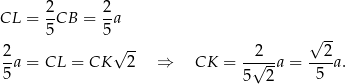
CL = 2CB = 2-a 5 5 √ -- 2 √ -- 2 2 -a = CL = CK 2 ⇒ CK = -√--a = ---a. 5 5 2 5

Stąd

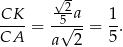
√-2 CK--= -5√-a-= 1. CA a 2 5

To oznacza, że 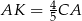AK = 4CA 5 i

CK 15 1 ----= 4-= -. AK 5 4
Wersja PDF