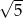/Szkoła średnia/Geometria/Planimetria/Czworokąt/Kwadrat

Zadanie nr 9309798

Dodaj do ulubionych
Dodaj do rozwiązanych

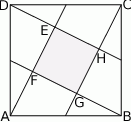
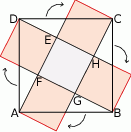
Wierzchołki kwadratu 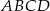ABCD połączono ze środkami jego boków (zobacz rysunek) i otrzymano w ten sposób mniejszy kwadrat 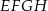EF GH . Oblicz, jaki jest stosunek obwodów kwadratów ABCD i EF GH .

PIC

Rozwiązanie

Oznaczmy długość boku dużego kwadratu przez a .

PIC

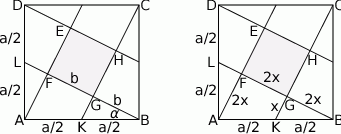
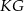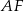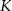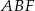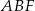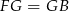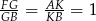Zauważmy, że odcinek KG jest równoległy do AF i przechodzi przez środek boku K trójkąta ABF . Jest to więc odcinek łączący środki boków w trójkącie ABF , czyli FG = GB (inny sposób uzasadnienia tej równości, to zastosowanie twierdzenia Talesa: FG- AK- GB = KB = 1 ).

Sposób I

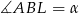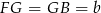Jeżeli oznaczymy ∡ABL = α i FG = GB = b , to z trójkąta prostokątnego 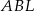ABL mamy

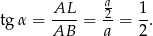
AL a2 1 tg α = ----= --= --. AB a 2

Patrzymy teraz na trójkąt prostokątny 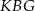KBG .

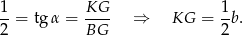
1- KG-- 1- 2 = tgα = BG ⇒ KG = 2b.

Piszemy teraz twierdzenie Pitagorasa w trójkącie 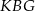KBG .

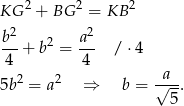
KG 2 + BG 2 = KB 2 2 2 b-+ b2 = a-- / ⋅4 4 4 2 2 √a-- 5b = a ⇒ b = 5.

W takim razie stosunek obwodów kwadratów jest równy

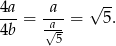
4a a √ -- 4b-= √a- = 5. 5

Sposób II

Tym razem obejdziemy się bez trygonometrii. Jak zauważyliśmy na początku, odcinek 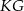KG łączy środki boków w trójkącie 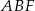ABF , więc w szczególności 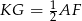KG = 12AF . Podobnie uzasadniamy, że odcinek 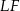LF łączy środki boków w trójkącie 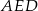AED , więc 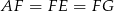AF = FE = FG . Jeżeli więc oznaczymy 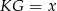KG = x , to mamy

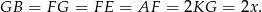
GB = F G = FE = AF = 2KG = 2x.

Piszemy teraz twierdzenie Pitagorasa w trójkącie 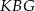KBG .

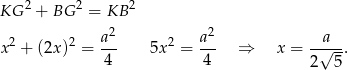
KG 2 + BG 2 = KB 2 2 2 x2 + (2x )2 = a-- 5x2 = a-- ⇒ x = -a√--. 4 4 2 5

W takim razie stosunek obwodów kwadratów jest równy

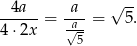
4a a √ -- ------= -a--= 5. 4⋅2x √5

Sposób III

Tym razem zauważmy, że duży kwadrat można rozciąć w ten sposób, że z otrzymanych części można złożyć 5 kwadratów takich samych jak mały kwadrat. To oznacza, że pole dużego kwadratu jest 5 razy większe od pola małego kwadratu, czyli jego bok jest 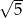√ -- 5 razy dłuższy niż bok małego kwadratu. Oczywiście stosunek obwodów też jest równy √ -- 5 .

PIC

 
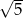Odpowiedź: √ -- 5

Wersja PDF