/Szkoła średnia/Geometria/Stereometria/Stożek/Inne

Zadanie nr 4152065

Dodaj do ulubionych
Dodaj do rozwiązanych

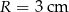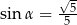Metalową kulę o promieniu R = 3 cm przetopiono na stożek. Tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem α , takim, że √ - sinα = --5 5 . Wyznacz promień podstawy tego stożka.

Rozwiązanie

Zaczynamy od rysunku

PIC

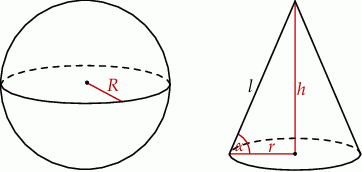
Najpierw liczymy objętość kuli

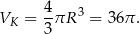
VK = 4-πR 3 = 36π . 3

Z założeń mamy

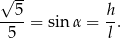
√ -- --5-= sin α = h-. 5 l

Długość tworzącej 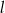l możemy wyznaczyć z twierdzenia Pitagorasa

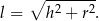
∘ ------- l = h 2 + r2.

Zatem otrzymujemy układ równań

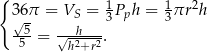
{ 1 1 2 3√6π = VS = 3Pph = 3πr h --5 = √--h---. 5 h2+r2

Przekształcamy pierwsze równanie

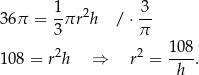
1 3 36 π = -πr 2h / ⋅-- 3 π 10 8 = r2h ⇒ r2 = 1-08. h

Teraz przekształcamy drugie równanie i następnie podstawimy wynik z pierwszego

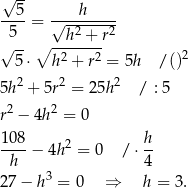
√ -- --5- ----h---- 5 = √h-2-+-r2 √ -- ∘ ------- 5 ⋅ h2 + r2 = 5h /()2 2 2 2 5h + 5r = 25h / : 5 r2 − 4h2 = 0 108-− 4h2 = 0 / ⋅ h- h 4 27 − h3 = 0 ⇒ h = 3.

Zatem

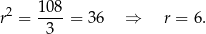
2 108 r = ----= 36 ⇒ r = 6 . 3

 
Odpowiedź: 6

Wersja PDF