Zadanie nr 9485246
W stożek o promieniu podstawy długości 10 i wysokości 15 wpisano walec, w ten sposób, że jedna podstawa walca zawiera się w podstawie stożka, a brzeg jego drugiej podstawy zawiera się w powierzchni bocznej stożka. Oblicz długość promienia podstawy i długość wysokości walca, wiedząc że pole powierzchni bocznej walca wynosi 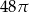 .
.
Rozwiązanie
Rysujemy przekrój osiowy stożka i oznaczmy przez 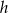 i
i  wysokość i promień walca.
wysokość i promień walca.
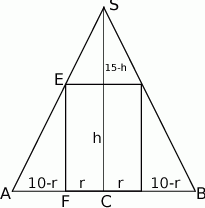
Z informacji o polu powierzchni bocznej walca mamy

Korzystamy teraz z podobieństwa trójkątów 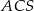 i
i 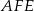 .
.
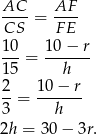
Podstawiamy to teraz do równości 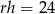 .
.
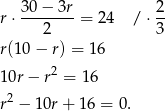
Liczymy 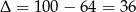 ,
, 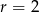 lub
lub 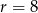 . Stąd
. Stąd 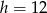 lub
lub 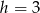 odpowiednio.
odpowiednio.
Odpowiedź: 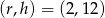 lub
lub