Zadanie nr 2812723
Na wysokości 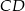 trójkąta
trójkąta 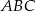 wybrano punkt
wybrano punkt 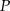 taki, że
taki, że 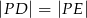 , gdzie
, gdzie 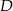 i
i 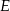 są rzutami tego punktu odpowiednio na boki
są rzutami tego punktu odpowiednio na boki 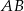 i
i 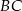 . Wiedząc, że
. Wiedząc, że 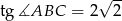 oblicz iloraz
oblicz iloraz  .
.
Rozwiązanie
Rozpoczynamy oczywiście od rysunku.
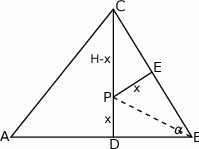
Sposób I
Zauważmy, że trójkąty prostokątne 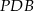 i
i 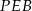 mają równe dwa boki, więc są przystające. Zatem
mają równe dwa boki, więc są przystające. Zatem 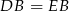 . Ponadto, patrząc na trójkąt
. Ponadto, patrząc na trójkąt 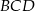 mamy
mamy
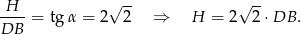
Pisząc twierdzenie Pitagorasa w tym samym trójkącie mamy
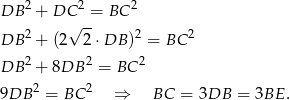
To oznacza, że
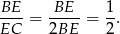
Sposób II
Zauważmy, że trójkąty 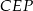 i
i 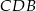 są oba prostokątne i mają wspólny kąt
są oba prostokątne i mają wspólny kąt 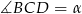 , więc są podobne. Używając tego podobieństwa oraz podanego tangensa, wyliczymy długości odcinków
, więc są podobne. Używając tego podobieństwa oraz podanego tangensa, wyliczymy długości odcinków 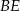 i
i 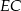 w zależności od
w zależności od 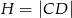 .
.
Zauważmy od razu, że
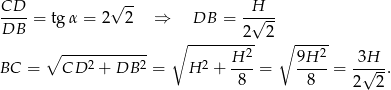
Z podobieństwa trójkątów 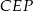 i
i 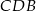 mamy
mamy
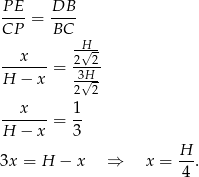
Teraz łatwo wyliczyć długości odcinków 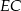 i
i 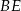 . Możemy wykorzystać twierdzenie Pitagorasa w trójkącie
. Możemy wykorzystać twierdzenie Pitagorasa w trójkącie 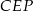 , ale możemy też raz jeszcze skorzystać z podobieństwa.
, ale możemy też raz jeszcze skorzystać z podobieństwa.
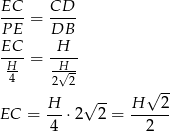
Stąd
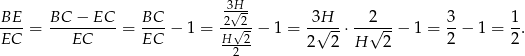
Odpowiedź: