/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Długości odcinków

Zadanie nr 4518232

Trójkąt 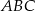ABC podzielony jest przez dwie proste równoległe do boku 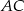AC , na trzy figury o równych polach. Oblicz na jakie części proste te podzieliły bok AB = a .

Wersja PDF

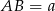Rozwiązanie

Przyjmijmy oznaczenia z rysunku.

PIC

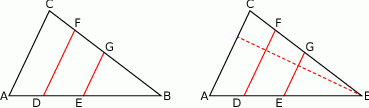
Sposób I

Skoro trzy otrzymane części mają równe pola, mamy

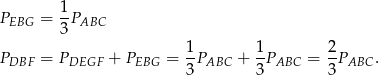
PEBG = 1-PABC 3 1- 1- 2- PDBF = PDEGF + PEBG = 3PABC + 3PABC = 3PABC .

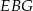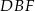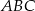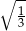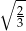Oczywiście trójkąty EBG i DBF są podobne do trójkąta ABC , a powyższe równości pozwalają obliczyć skale podobieństwa, są one równe odpowiednio: ∘ -- 13 i ∘ -- 23 (bo pole zmienia się jak kwadrat skali podobieństwa). W takim razie

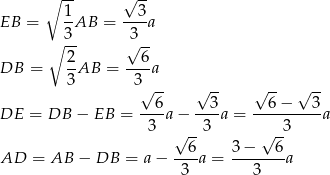
∘ -- √ -- 1 3 EB = --AB = ----a ∘ 3- 3√ -- 2- --6- DB = 3AB = 3 a √ -- √ -- √ -- √ -- DE = DB − EB = --6a − --3-a = --6-−---3a 3 3 3 √ 6- 3 − √ 6- AD = AB − DB = a − ----a = -------a 3 3

Sposób II

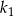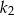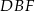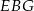Oznaczmy przez k1 i k2 skale podobieństwa odpowiednio trójkątów DBF i EBG do trójkąta 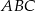ABC . W takim razie

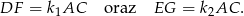
DF = k1AC oraz EG = k2AC .

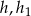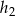Jeżeli oznaczmy przez h,h1 i h2 wysokości trójkątów 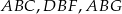ABC ,DBF ,ABG opuszczone z wierzchołka 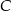C , to mamy również

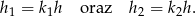
h = k h oraz h = k h. 1 1 2 2

Korzystamy teraz z podanej równości pól.

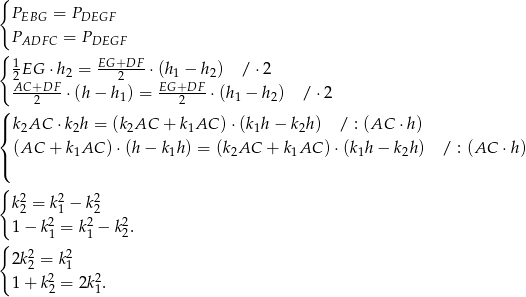
{ PEBG = PDEGF PADFC = PDEGF { 12EG ⋅h2 = EG+D2F--⋅(h1 − h2) / ⋅2 AC-+DF-⋅ (h− h ) = EG-+DF-⋅(h − h ) / ⋅2 ( 2 1 2 1 2 | k2AC ⋅k2h = (k2AC + k1AC )⋅(k1h − k2h) / : (AC ⋅h) { | (AC + k 1AC )⋅ (h− k1h) = (k2AC + k1AC )⋅(k1h − k2h ) / : (AC ⋅h) ( { k22 = k21 − k22 1 − k2 = k2 − k2. { 1 1 2 2k2 = k 2 2 2 1 2 1 + k2 = 2k 1.

Podstawiamy teraz 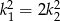2 2 k1 = 2k2 z pierwszego równania do drugiego.

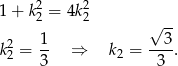
1+ k2= 4k2 2 2 √ -- 2 1- --3- k2 = 3 ⇒ k2 = 3 .

Stąd

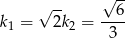
√ -- √ -- 6 k1 = 2k2 = -3--

oraz

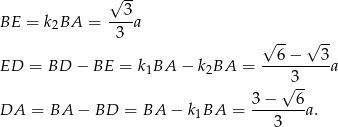
√ -- BE = k2BA = --3a 3 √ -- √ -- 6− 3 ED = BD − BE = k1BA − k2BA = ---------a √ 3- 3-−---6- DA = BA − BD = BA − k 1BA = 3 a.

 
Odpowiedź: √- √- √- √ - 3−--6a ,-6−--3a,--3a 3 3 3

Wersja PDF