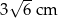Zadanie nr 5287176
W trójkącie ostrokątnym 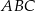 bok
bok 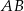 ma długość 18 cm, a wysokość
ma długość 18 cm, a wysokość 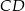 jest równa 15 cm. Punkt
jest równa 15 cm. Punkt 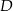 dzieli bok
dzieli bok 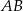 tak, że
tak, że 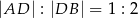 . Przez punkt
. Przez punkt 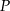 leżący na odcinku
leżący na odcinku 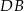 poprowadzono prostą równoległą do prostej
poprowadzono prostą równoległą do prostej 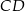 , odcinając od trójkąta
, odcinając od trójkąta 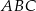 trójkąt, którego pole jest cztery razy mniejsze niż pole trójkąta
trójkąt, którego pole jest cztery razy mniejsze niż pole trójkąta 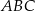 . Oblicz długość odcinka
. Oblicz długość odcinka 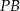 .
.
Rozwiązanie
Zaczynamy oczywiście od rysunku.
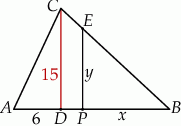
Ponieważ 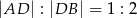 i
i 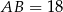 , mamy
, mamy
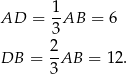
Pole trójkąta 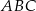 jest równe
jest równe
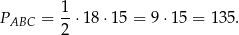
Zatem pole trójkąta 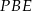 jest równe
jest równe
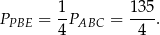
Sposób I
Zauważmy, że trójkąty 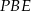 i
i 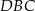 są podobne. Pole pierwszego już znamy, a pole drugiego możemy łatwo wyliczyć
są podobne. Pole pierwszego już znamy, a pole drugiego możemy łatwo wyliczyć
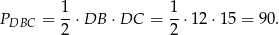
Ponieważ pole zmienia się jak kwadrat skali podobieństwa, więc skala 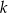 podobieństwa tych trójkątów jest równa
podobieństwa tych trójkątów jest równa
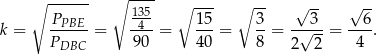
Mamy zatem
Sposób II
Jeżeli oznaczymy 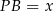 i
i 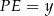 to wyliczonego pola trójkąta
to wyliczonego pola trójkąta 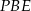 mamy
mamy
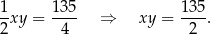
Tak jak poprzednio zauważamy, że trójkąty 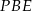 i
i 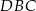 są podobne, ale tym razem nie wyliczamy ich skali podobieństwa, tylko od razu piszemy iloraz odpowiadających boków.
są podobne, ale tym razem nie wyliczamy ich skali podobieństwa, tylko od razu piszemy iloraz odpowiadających boków.
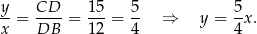
Podstawiamy tę wartość do poprzedniego równania
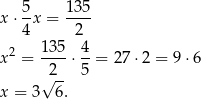
Odpowiedź: