/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Długości odcinków

Zadanie nr 5355781

W trójkącie 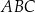ABC , w którym 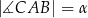|∡CAB | = α , poprowadzono dwusieczną 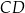CD kąta wewnętrznego 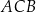ACB , przy czym 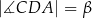|∡CDA | = β . Oblicz |AD-| |DB| .

Wersja PDF

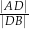Rozwiązanie

Zacznijmy od rysunku.

PIC

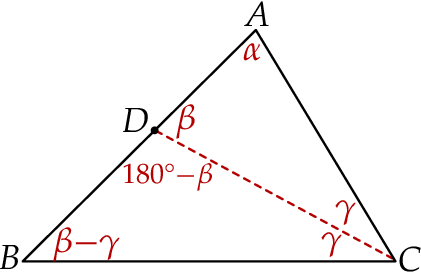
Jeżeli oznaczymy

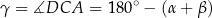
γ = ∡DCA = 180 ∘ − (α + β )

to mamy

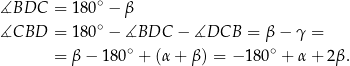
∘ ∡BDC = 180 − β ∡CBD = 180∘ − ∡BDC − ∡DCB = β − γ = ∘ ∘ = β − 180 + (α + β ) = − 180 + α + 2β.

Teraz korzystamy z twierdzenia sinusów.

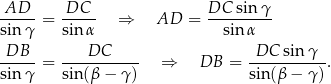
-AD-- = DC--- ⇒ AD = DC--sin-γ- sin γ sin α sinα DB DC DC sin γ ----- = ----------- ⇒ DB = -----------. sin γ sin (β − γ) sin(β − γ)

Zatem

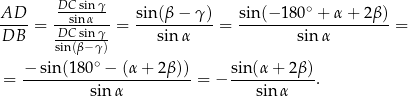
DC-sinγ- ∘ AD-- = --sinα-- = sin-(β−--γ)-= sin-(−-180--+-α-+-2β)-= DB DC-sinγ-- sin α sin α sin(β −γ) −-sin(18-0∘ −-(α+--2β)) sin-(α+--2β)- = sin α = − sinα .

Oczywiście ta liczba nie jest ujemna, po prostu 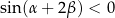sin(α + 2β ) < 0 .

Zamiast korzystać z twierdzenia sinusów, mogliśmy od razu skorzystać z twierdzenia o dwusiecznej – rozwiązanie byłoby wtedy odrobinę krótsze.  
Odpowiedź: − sin(α+-2β) sinα

Wersja PDF