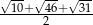/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Długości odcinków

Zadanie nr 5640664

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz sumę długości środkowych trójkąta o długościach boków: 2, 3 i 4.

Rozwiązanie

Szkicujemy trójkąt i jego środkowe.

PIC

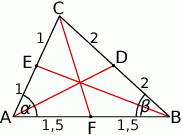
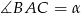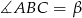Długości środkowych obliczymy korzystając z twierdzenia cosinusów, ale zanim to zrobimy, obliczymy cosinusy kątów wewnętrznych trójkąta. Jeżeli oznaczymy ∡BAC = α i ∡ABC = β , to na mocy twierdzenia cosinusów mamy

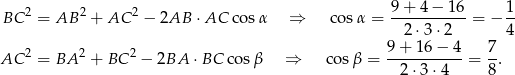
2 2 2 9 + 4 − 16 1 BC = AB + AC − 2AB ⋅ AC co sα ⇒ cosα = -----------= − -- 2⋅ 3⋅2 4 AC 2 = BA 2 + BC 2 − 2BA ⋅BC cosβ ⇒ co sβ = 9+--16−--4-= 7-. 2 ⋅3 ⋅4 8

Teraz pozostało zastosować twierdzenie cosinusów w trójkątach 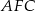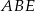AF C , ABE i ABD .

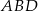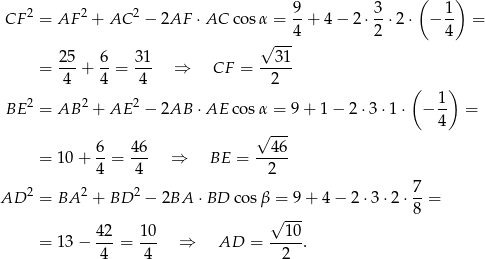
( ) 2 2 2 9 3 1 CF = AF + AC − 2AF ⋅AC cosα = 4-+ 4 − 2 ⋅2-⋅2⋅ − 4- = √ --- 25- 6- 31- --31- = 4 + 4 = 4 ⇒ CF = 2 ( ) BE 2 = AB 2 + AE 2 − 2AB ⋅AE cosα = 9+ 1− 2 ⋅3 ⋅1 ⋅ − 1- = 4 6 46 √ 46- = 10+ --= --- ⇒ BE = ----- 4 4 2 AD 2 = BA 2 + BD 2 − 2BA ⋅BD cosβ = 9+ 4− 2⋅3 ⋅2 ⋅ 7-= 8 42 10 √ 10- = 13− ---= --- ⇒ AD = ----. 4 4 2

Suma długości środkowych jest więc równa

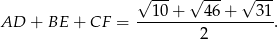
√ --- √ --- √ --- 10+ 46 + 31 AD + BE + CF = ------------------. 2

 
Odpowiedź: -- -- -- √-10+√-46+-√31 2

Wersja PDF