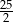Zadanie nr 6162865
Na trójkącie o bokach długości 15, 20, 25 opisano okrąg. Oblicz długość środkowej tego trójkąta poprowadzonej do środka najdłuższego boku.
Rozwiązanie
Gdy przyjrzymy się podanym długościom boków, to powinniśmy zauważyć, że dany trójkąt jest prostokątny (jest to trójkąt 5 razy większy od trójkąta o bokach 3, 4, 5).
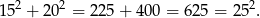
Szkicujemy trójkąt prostokątny.
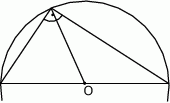
Zauważmy teraz, że okrąg o średnicy będącej przeciwprostokątną trójkąta to dokładnie okrąg opisany na trójkącie (bo kąt oparty na średnicy jest prosty). W takim razie środkowa poprowadzona z kąta prostego jest promieniem okręgu opisanego, czyli ma długość równą połowie przeciwprostokątnej.
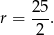
Odpowiedź: