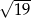Zadanie nr 6303090
W trójkącie  dane są:
dane są: 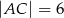 ,
, 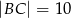 i kąt
i kąt 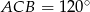 . Wyznacz długość środkowej
. Wyznacz długość środkowej 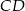 tego trójkąta.
tego trójkąta.
Rozwiązanie
Zaczynamy od rysunku.
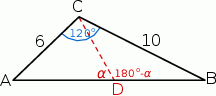
Plan jest następujący: najpierw obliczymy (z twierdzenia cosinusów) długość boku 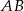 , a potem spróbujemy wykorzystać to, że odcinek
, a potem spróbujemy wykorzystać to, że odcinek 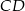 jest wspólnym bokiem w dwóch trójkątach, w których znamy wszystkie pozostałe długości boków.
jest wspólnym bokiem w dwóch trójkątach, w których znamy wszystkie pozostałe długości boków.
Długość boku 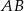 obliczamy stosując twierdzenie cosinusów w trójkącie
obliczamy stosując twierdzenie cosinusów w trójkącie 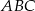 .
.
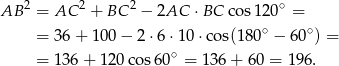
Sąd 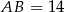 .
.
Próbujemy teraz napisać twierdzenia cosinusów w trójkątach 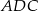 i
i 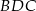 tak, żeby otrzymać układ równań, z którego obliczymy
tak, żeby otrzymać układ równań, z którego obliczymy 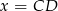 . Trzeba jednak przy tym trochę uważać i wybrać odpowiednie kąty do twierdzenia cosinusów tak, aby móc je potem wyeliminować. Oznaczmy
. Trzeba jednak przy tym trochę uważać i wybrać odpowiednie kąty do twierdzenia cosinusów tak, aby móc je potem wyeliminować. Oznaczmy 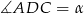 . Wtedy
. Wtedy 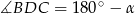 i
i
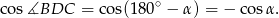
Piszemy teraz twierdzenia cosinusów w trójkątach 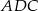 i
i 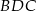 .
.
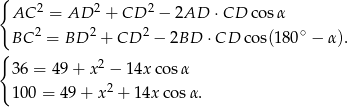
Dodajemy teraz te równania stronami (żeby skrócić  ) i mamy
) i mamy
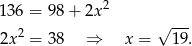
Odpowiedź: