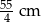Zadanie nr 8332916
W trójkącie 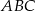 wysokość
wysokość 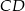 dzieli bok
dzieli bok 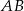 na odcinki długości
na odcinki długości 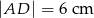 i
i 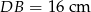 . Bok
. Bok 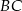 ma 20 cm długości. Poprowadzono symetralną boku
ma 20 cm długości. Poprowadzono symetralną boku 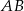 . Wyznacz długości odcinków, na jakie symetralna ta podzieliła bok
. Wyznacz długości odcinków, na jakie symetralna ta podzieliła bok 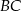 .
.
Rozwiązanie
Niech 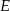 będzie środkiem boku
będzie środkiem boku 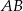 , a
, a 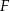 niech będzie punktem wspólnym symetralnej boku
niech będzie punktem wspólnym symetralnej boku 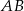 i boku
i boku 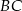 .
.
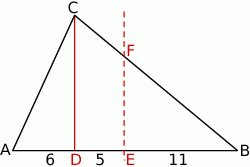
Punkt 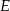 jest środkiem boku
jest środkiem boku  , więc
, więc
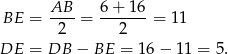
Na mocy twierdzenia Talesa,
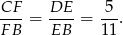
To oznacza, że
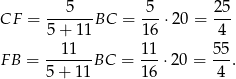
Odpowiedź: 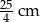 i
i