Zadanie nr 9620703
Na trójkącie 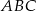 , w którym
, w którym 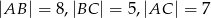 opisano okrąg o środku
opisano okrąg o środku 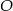 . Następnie poprowadzono styczną
. Następnie poprowadzono styczną 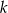 do okręgu w punkcie
do okręgu w punkcie 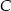 , która w punkcie
, która w punkcie 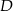 przecięła prostą zawierającą bok
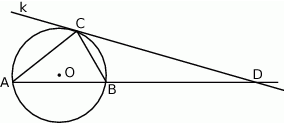
przecięła prostą zawierającą bok 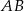 (jak na rysunku poniżej). Oblicz odległość punktu
(jak na rysunku poniżej). Oblicz odległość punktu 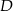 od wierzchołka
od wierzchołka 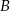 , jeżeli wiadomo, że
, jeżeli wiadomo, że 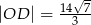 .
.
Rozwiązanie
Spróbujmy na początku ustalić jaki będzie plan działania.
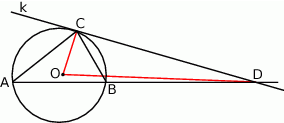
Na mocy twierdzenia o odcinkach siecznych (lub jak ktoś woli z podobieństwa trójkątów 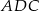 i
i 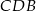 ) mamy
) mamy
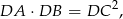
co oznacza, że łatwo wyliczymy długość odcinka 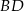 jeżeli tylko będziemy znali długość odcinka stycznej
jeżeli tylko będziemy znali długość odcinka stycznej 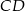 . Tę długość jednak łatwo wyliczyć z trójkąta prostokątnego
. Tę długość jednak łatwo wyliczyć z trójkąta prostokątnego 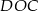 , pod warunkiem, że znamy długość promienia okręgu opisanego na trójkącie
, pod warunkiem, że znamy długość promienia okręgu opisanego na trójkącie 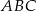 – ten promień da się wyliczyć, bo znamy długości wszystkich boków trójkąta
– ten promień da się wyliczyć, bo znamy długości wszystkich boków trójkąta 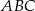 .
.
Mamy plan działania, więc do dzieła. Rozpocznijmy od wyliczenia pola trójkąta 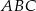 - korzystamy ze wzoru Herona
- korzystamy ze wzoru Herona
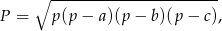
gdzie 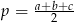 jest połową obwodu. W naszej sytuacji mamy
jest połową obwodu. W naszej sytuacji mamy
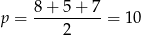
oraz
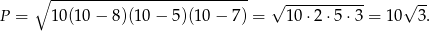
Teraz korzystamy ze wzoru na pole 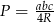 , skąd mamy
, skąd mamy
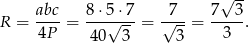
Teraz z trójkąta prostokątnego 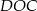 mamy
mamy
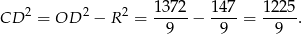
Teraz pozostało wyliczyć 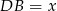 . Mamy
. Mamy
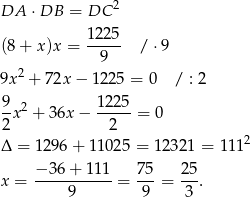
Odpowiedź: