Zadanie nr 1178334
Dla jakich wartości parametru 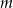 , odwrotność sumy pierwiastków równania
, odwrotność sumy pierwiastków równania
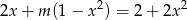
jest dodatnia?
Rozwiązanie
Zapiszmy równanie w postaci ogólnej.
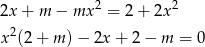
Na początek zobaczmy co się dzieje, gdy równanie nie jest kwadratowe, czyli dla 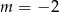 . Mamy wtedy równanie
. Mamy wtedy równanie
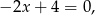
które ma pierwiastek dodatni 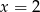 , czyli jest OK.
, czyli jest OK.
Jeżeli równanie jest kwadratowe, to sprawdźmy kiedy ma pierwiastki.
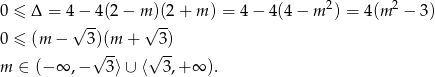
Na mocy wzorów Viète’a mamy
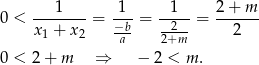
Uwzględniając warunek z 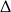 -ą i przypadek
-ą i przypadek 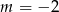 , mamy
, mamy
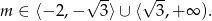
Zauważmy, że ten rachunek jest też poprawny, gdy równanie ma jeden pierwiastek podwójny 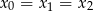 , czyli gdy
, czyli gdy 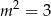 . Tak jest, bo wtedy
. Tak jest, bo wtedy
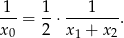
Odpowiedź: