/Szkoła średnia/Równania/Kwadratowe/Z parametrem

Zadanie nr 1641305

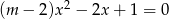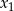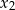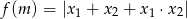Różnymi pierwiastkami równania kwadratowego 2 (m − 2)x − 2x + 1 = 0 są liczby x1 oraz x2 . Narysuj wykres funkcji f (m) = |x 1 + x 2 + x 1 ⋅x2| .

Wersja PDF

Rozwiązanie

Skoro mamy mieć równanie kwadratowe, to musi być 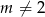m ⁄= 2 . Jeżeli ma mieć ono dwa różne pierwiastki, to musi być

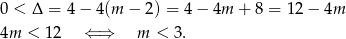
0 < Δ = 4 − 4 (m − 2) = 4 − 4m + 8 = 12− 4m 4m < 12 ⇐ ⇒ m < 3.

Przy powyższych założeniach możemy skorzystać ze wzorów Viète’a

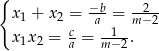
{ x1 + x2 = −b-= --2- c a-1--m −2 x1x2 = a = m− 2.

zatem interesująca nas funkcja ma wzór

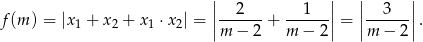
| | | | f(m ) = |x + x + x ⋅x | = ||--2---+ --1---||= ||--3---||. 1 2 1 2 |m − 2 m − 2| |m − 2|

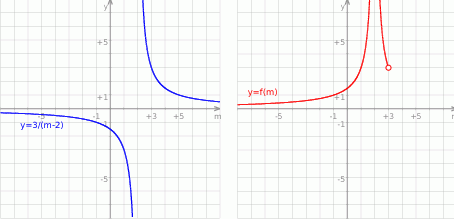
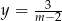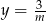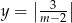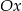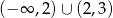Wykresem funkcji y = --3- m −2 jest hiperbola y = 3- m przesunięta o 2 jednostki w prawo. Aby otrzymać funkcję ||--3-|| y = m −2 należy część będącą pod osią Ox odbić do góry. Należy też pamiętać o obcięciu dziedziny do zbioru (− ∞ ,2) ∪ (2,3) .

PIC

Wersja PDF