Zadanie nr 1764493
Punkt 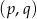 należy do zbioru
należy do zbioru  wtedy i tylko wtedy, gdy równanie
wtedy i tylko wtedy, gdy równanie 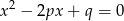 ma dwa różne rozwiązania
ma dwa różne rozwiązania 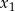 i
i 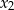 takie, że
takie, że 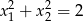 . Zaznacz w układzie współrzędnych zbiór
. Zaznacz w układzie współrzędnych zbiór 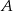 .
.
Rozwiązanie
Sprawdźmy najpierw kiedy równanie ma dwa różne pierwiastki
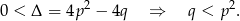
Skorzystamy teraz ze wzorów Viète’a
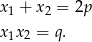
Liczymy
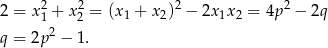
Zobaczmy teraz, co ta równość oznacza dla wcześniej uzyskanego warunku z 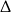 -y.
-y.
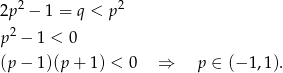
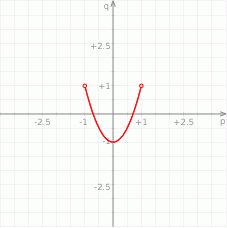
Szukany wykres to zatem parabola 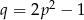 obcięta do przedziału
obcięta do przedziału 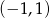 .
.