/Szkoła średnia/Równania/Kwadratowe/Z parametrem

Zadanie nr 1794591

Dodaj do ulubionych
Dodaj do rozwiązanych

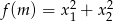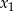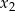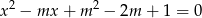Wyznacz dziedzinę i naszkicuj wykres funkcji 2 2 f(m ) = x 1 + x 2 , gdzie x1 i x2 są różnymi pierwiastkami równania x 2 − mx + m 2 − 2m + 1 = 0 .

Rozwiązanie

Na mocy wzorów Viète’a mamy

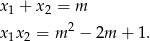
x + x = m 1 2 x1x2 = m 2 − 2m + 1.

Mamy zatem

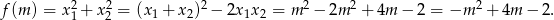
f(m ) = x2 + x2 = (x + x2)2− 2x x2 = m 2− 2m 2+ 4m − 2 = −m 2+ 4m − 2. 1 2 1 1

Aby wyznaczyć dziedzinę tej funkcji musimy ustalić dla jakich wartości 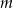m podane równanie ma dwa rozwiązania. Tak będzie o ile Δ > 0 .

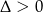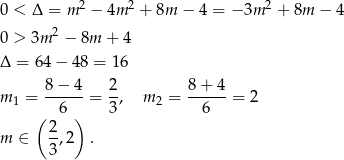
0 < Δ = m2 − 4m 2 + 8m − 4 = − 3m 2 + 8m − 4 2 0 > 3m − 8m + 4 Δ = 64 − 48 = 16 8− 4 2 8 + 4 m 1 = ------= --, m 2 = ------= 2 ( 6 ) 3 6 2- m ∈ 3 ,2 .

Aby narysować wykres funkcji 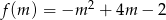f(m ) = −m 2 + 4m − 2 zauważmy, że 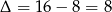Δ = 16 − 8 = 8 i jej wierzchołek ma współrzędne

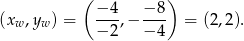
( − 4 − 8) (xw ,yw) = ----,− ---- = (2,2). − 2 − 4

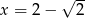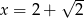Ponadto jej miejsca zerowe to √ -- x = 2− 2 i √ -- x = 2 + 2 . Teraz bez trudu rysujemy żądany wykres.

PIC

 
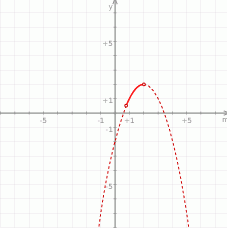
Odpowiedź: ( ) Df = 23,2

Wersja PDF