/Szkoła średnia/Równania/Kwadratowe/Z parametrem

Zadanie nr 2613037

Dla jakich wartości parametru 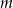m równanie 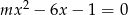2 mx − 6x − 1 = 0 ma co najmniej jedno rozwiązanie?

Wersja PDF

Rozwiązanie

Sprawdźmy najpierw co się dzieje dla 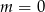m = 0 (gdy równanie jest liniowe). Wtedy mamy równanie 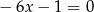− 6x− 1 = 0 , które ma jedno rozwiązanie.

Jeżeli równanie jest kwadratowe, to ma co najmniej jedno rozwiązanie jeżeli 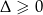Δ ≥ 0 . Liczymy

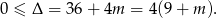
0 ≤ Δ = 36 + 4m = 4 (9+ m ).

Rozwiązaniem tej nierówności jest zbiór 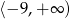⟨− 9,+ ∞ ) .  
Odpowiedź: m ∈ ⟨− 9,+ ∞ )

Wersja PDF