/Szkoła średnia/Równania/Kwadratowe/Z parametrem

Zadanie nr 2628312

Dane są liczby wymierne 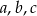a,b,c takie, że równanie 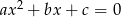2 ax + bx + c = 0 ma dwa rozwiązania rzeczywiste. Uzasadnij, że jeżeli jeden z pierwiastków tego równania jest liczbą wymierną to drugi pierwiastek też jest liczbą wymierną.

Wersja PDF

Rozwiązanie

Sposób I

Pierwiastki danego równania kwadratowego są postaci

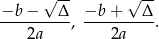
√ -- √ -- −b--−---Δ-, −b-+----Δ. 2a 2a

Zauważmy, że jeżeli jeden z nich jest liczbą wymierną, to wymierna jest też liczba 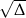√ -- Δ . Rzeczywiście, jeżeli np. 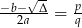√ -- −b-−--Δ = p 2a q , gdzie 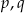p,q liczby całkowite to

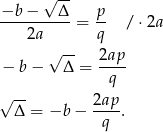
√ -- −b − Δ p ----------= -- / ⋅2a 2a q √ -- 2ap- − b− Δ = q √ -- Δ = −b − 2ap. q

To jednak oznacza, że obie liczby

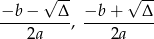
√ -- √ -- −b-−---Δ-- −b-+----Δ- 2a , 2a

są wymierne.

Sposób II

Jeżeli 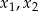x1,x2 są pierwiastakmi danego równania, to na mocy wzorów Viéte’a mamy

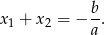
b- x1 + x2 = − a .

Z prawej strony tej równości jest liczba wymierna, więc jeżeli jeden z pierwiastków jest liczbą wymierną to drugi też.

Wersja PDF