/Szkoła średnia/Równania/Kwadratowe/Z parametrem

Zadanie nr 2689591

Dodaj do ulubionych
Dodaj do rozwiązanych

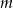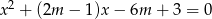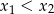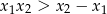Dla jakich wartości parametru m równanie 2 x + (2m − 1)x − 6m + 3 = 0 ma dwa różne pierwiastki x 1 < x2 spełniające nierówność x1x2 > x2 − x1 .

Rozwiązanie

Sprawdźmy najpierw kiedy równanie ma dwa różne rozwiązania.

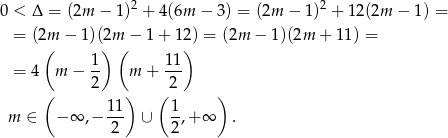
2 2 0 < Δ = (2m − 1) + 4(6m − 3) = (2m − 1) + 12(2m − 1) = = (2m − 1 )(2m − 1 + 12 ) = (2m − 1 )(2m + 11 ) = ( 1) ( 11) = 4 m − -- m + --- ( 2 ) (2 ) 11 1 m ∈ − ∞ ,− --- ∪ -,+ ∞ . 2 2

Sposób I

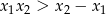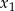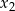Popatrzmy teraz na daną nierówność: x1x2 > x2 − x1 . Nierówność ta nie jest symetryczna ze względu na x1 i x 2 , więc nie możemy bezpośrednio zastosować wzorów Viète’a, ale będziemy mogli to zrobić gdy podniesiemy nierówność do kwadratu. Aby to zrobić musimy jednak wiedzieć, że obie strony nierówności są dodatnie. Prawa strona jest dodatnia z założenia, więc jeżeli lewa strona jest ujemna to nierówność jest sprzeczna. Na mocy wzorów Viète’a musi więc być spełniony warunek

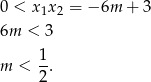
0 < x1x2 = − 6m + 3 6m < 3 m < 1. 2

Przy tym założeniu możemy podnieść nierówność stronami do kwadratu.

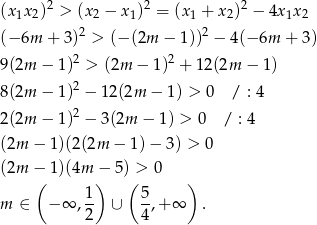
(x 1x 2)2 > (x2 − x1)2 = (x1 + x2)2 − 4x1x2 2 2 (− 6m + 3) > (− (2m − 1)) − 4(− 6m + 3) 9(2m − 1)2 > (2m − 1)2 + 12(2m − 1) 8(2m − 1)2 − 12(2m − 1) > 0 / : 4 2 2(2m − 1) − 3(2m − 1) > 0 / : 4 (2m − 1)(2(2m − 1) − 3) > 0 (2m −( 1)(4m )− 5)(> 0 ) 1- 5- m ∈ − ∞ ,2 ∪ 4 ,+ ∞ .

W połączeniu z poprzednimi ograniczeniami otrzymujemy więc 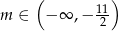( ) m ∈ − ∞ ,− 112 .

Sposób II

Skoro 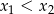x 1 < x2 to

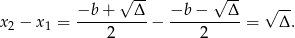
√ -- √ -- −b--+---Δ- −b--−---Δ- √ -- x2 − x1 = 2 − 2 = Δ .

Na mocy wzorów Viète’a możemy więc daną nierówność zapisać w postaci

− 6m + 3 > √ Δ-.

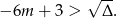
Jeżeli lewa strona jest ujemna to nierówność jest sprzeczna, więc załóżmy, że

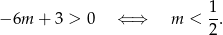
1 − 6m + 3 > 0 ⇐ ⇒ m < --. 2

Przy tym założeniu mamy

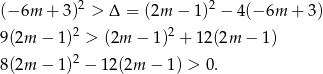
(− 6m + 3 )2 > Δ = (2m − 1)2 − 4(− 6m + 3) 9(2m − 1)2 > (2m − 1)2 + 12(2m − 1) 2 8(2m − 1) − 12(2m − 1) > 0.

Dalej liczymy jak w I sposobie.  
Odpowiedź: ( ) m ∈ − ∞ ,− 11 2

Wersja PDF