/Szkoła średnia/Równania/Kwadratowe/Z parametrem

Zadanie nr 2757248

Dodaj do ulubionych
Dodaj do rozwiązanych

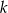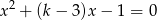Znajdź zbiór tych wartości parametru k , dla których dane równanie ma dwa różne pierwiastki x 2 + (k − 3)x − 1 = 0 .

Rozwiązanie

Podane równanie ma dwa różne pierwiastki jeżeli 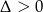Δ > 0 . Liczymy

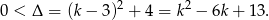
2 2 0 < Δ = (k− 3 ) + 4 = k − 6k+ 13.

Rozwiązujemy otrzymaną nierówność kwadratową, 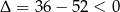Δ = 3 6− 5 2 < 0 . Nierówność ta jest więc zawsze prawdziwa.  
Odpowiedź: k ∈ R

Wersja PDF