Równanie kwadratowe to równanie postaci
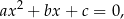
gdzie 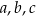 pewne liczby i
pewne liczby i 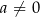 . Jeżeli
. Jeżeli 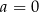 to w równaniu nie ma
to w równaniu nie ma 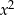 i równanie jest liniowe. Przykłady Równanie kwadratowe może mieć 0,1 lub 2 rozwiązania.
i równanie jest liniowe. Przykłady Równanie kwadratowe może mieć 0,1 lub 2 rozwiązania.
| Ilość rozwiązań | Przykład |
| 0 | 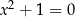 , lewa strona jest zawsze dodatnia. , lewa strona jest zawsze dodatnia. |
| 1 | 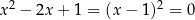 , rozwiązanie , rozwiązanie 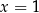 . . |
| 2 | 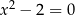 , rozwiązania , rozwiązania 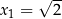 i i 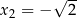 . . |
W przypadku prostych równań (jak te powyżej) rozwiązania możemy znaleźć wprost, na przykład
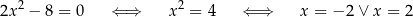
Delta Jeżeli równanie jest bardziej skomplikowane to o ilości rozwiązań mówi nam 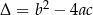 .
.
Znak 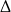 -y -y | Rozwiązania równania |
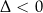 | Brak rozwiązań. |
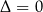 | Jedno rozwiązanie: 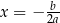 . . |
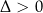 | Dwa rozwiązania: 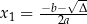 i i 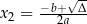 . . |
Spróbujmy ustalić liczbę rozwiązań równania
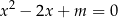
w zależności od parametru 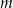 . Ponieważ
. Ponieważ 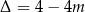 równanie ma dwa rozwiązania dla
równanie ma dwa rozwiązania dla 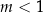 , jedno rozwiązanie dla
, jedno rozwiązanie dla 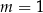 i nie ma rozwiązań dla
i nie ma rozwiązań dla 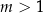 .
.
Stosując wzory z 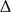 -ą należy pamiętać o ważnym założeniu
-ą należy pamiętać o ważnym założeniu 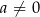 . O ile w przypadku zwykłych równań nie problemu, bo widać czy jest
. O ile w przypadku zwykłych równań nie problemu, bo widać czy jest 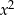 czy go nie ma, to w przypadku równań z parametrem, musimy zawsze osobno sprawdzić co się dzieje, gdy współczynnik przy
czy go nie ma, to w przypadku równań z parametrem, musimy zawsze osobno sprawdzić co się dzieje, gdy współczynnik przy 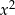 jest zerowy – inaczej powyższe wzory nie mają sensu (wszędzie w mianowniku jest
jest zerowy – inaczej powyższe wzory nie mają sensu (wszędzie w mianowniku jest  ).
).
Równanie
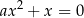
ma jedno rozwiązanie dla 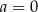 , pomimo że dla
, pomimo że dla 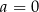 mamy
mamy 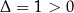 .
.
Sprawdźmy kiedy równanie
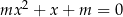
ma dokładnie jedno rozwiązanie. Najpierw sprawdzamy przypadek 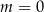 – otrzymane równanie liniowe ma dokładnie jedno rozwiązanie. Pozostaje sprawdzić, kiedy
– otrzymane równanie liniowe ma dokładnie jedno rozwiązanie. Pozostaje sprawdzić, kiedy 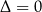 – okazuje się, że dla
– okazuje się, że dla 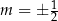 .
.
Ostateczną odpowiedzią jest więc 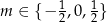 .
.
Równanie dwukwadratowe Równanie dwukwadratowe to równanie wielomianowe stopnia 4 postaci
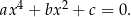
Dzięki temu, że w równaniu nie występuje  ani
ani 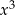 , równanie możemy łatwo sprowadzić do równania kwadratowego – wykonujemy podstawienie
, równanie możemy łatwo sprowadzić do równania kwadratowego – wykonujemy podstawienie 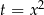 . Po tym podstawieniu otrzymujemy zwykłe równanie kwadratowe
. Po tym podstawieniu otrzymujemy zwykłe równanie kwadratowe
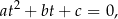
które rozwiązujemy używając 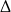 -y. Na koniec, gdy mamy wyliczone wartości
-y. Na koniec, gdy mamy wyliczone wartości 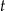 , musimy wyliczyć
, musimy wyliczyć  z równości
z równości 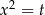 .
.
Rozwiążmy równanie
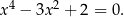
Po podstawieniu 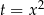 mamy równanie
mamy równanie
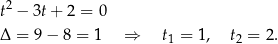
Daje nam to cztery pierwiastki wyjściowego równania:
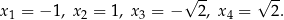
Tips & Tricks
1W przypadku równań z dużymi współczynnikami, które mają parzysty współczynnik przy  , zawsze warto podzielić równanie stronami przez 2 lub nawet przez 4.
, zawsze warto podzielić równanie stronami przez 2 lub nawet przez 4.
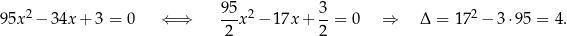
Na pierwszy rzut oka przekształcenie to wygląda groźnie, bo pojawiły się ułamki. Nie ma z tym jednak żadnego problemu, bo we wzorze na 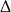 –ę jest
–ę jest 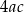 i ułamki znikną. We wzorach na pierwiastki też jest
i ułamki znikną. We wzorach na pierwiastki też jest 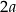 , więc nie ma problemu.
, więc nie ma problemu.
Przy odrobinie wprawy jest to niezwykle użyteczne uproszczenie.
2Podobnie jak przypadku równań wielomianowych, powinniśmy się nauczyć od ręki zauważać 1 lub 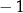 jako pierwiastek.
jako pierwiastek.
Jedynka jest pierwiastkiem, gdy suma współczynników jest zero, np. w równaniu
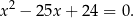
Dla 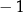 jest podobnie, tylko współczynnikowi przy
jest podobnie, tylko współczynnikowi przy  trzeba zmienić znak, np.
trzeba zmienić znak, np.
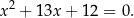
3Wzór na pierwiastek w przypadku 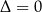 można łatwo zapamiętać na kilka sposobów: jest to dokładnie pierwsza współrzędna wierzchołka paraboli będącej wykresem równania, czyli
można łatwo zapamiętać na kilka sposobów: jest to dokładnie pierwsza współrzędna wierzchołka paraboli będącej wykresem równania, czyli 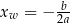 . Wystarczy więc pamiętać współrzędne wierzchołka. Jeszcze prostszy sposób to podstawienie
. Wystarczy więc pamiętać współrzędne wierzchołka. Jeszcze prostszy sposób to podstawienie 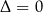 do wzorów z przypadku
do wzorów z przypadku 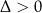 – wystarczy pamiętać te wzory.
– wystarczy pamiętać te wzory.
4W przypadku równania dwukwadratowego i podstawienia 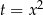 ważne jest, aby pamiętać, że musi być
ważne jest, aby pamiętać, że musi być 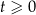 . Jak zwykle, nabiera to dużego znaczenia przy równaniach z parametrem.
. Jak zwykle, nabiera to dużego znaczenia przy równaniach z parametrem.
Sprawdźmy kiedy równanie
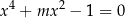
ma przynajmniej jedno rozwiązanie. Po podstawieniu 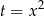 mamy równanie kwadratowe
mamy równanie kwadratowe
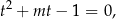
które musi mieć nieujemne rozwiązanie. Tak się składa, że to równanie kwadratowe ma zawsze dwa rozwiązania (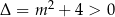 ) i zawsze jedno z nich jest dodatnie (ze wzorów Viète’a: iloczyn pierwiastków jest ujemny). Ogólnie sytuacja potrafi być jednak skomplikowana.
) i zawsze jedno z nich jest dodatnie (ze wzorów Viète’a: iloczyn pierwiastków jest ujemny). Ogólnie sytuacja potrafi być jednak skomplikowana.
5Równanie dwukwadratowe to nie jedyne równanie, które łatwo sprowadza się do równania kwadratowego. Podobna sytuacja ma miejsce zawsze, gdy umiemy równanie sprowadzić do postaci, w której jest pewne wyrażenie z niewiadomą i kwadrat tego wyrażania.
Rozwiążmy równanie
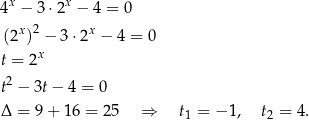
Ujemne rozwiązanie odrzucamy i mamy
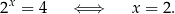
Rozwiążmy równanie 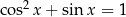 w przedziale
w przedziale 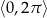
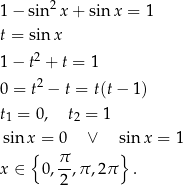
6Jeżeli równanie kwadratowe 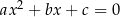 ma dwa pierwiastki
ma dwa pierwiastki 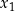 i
i 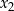 , to lewą stronę możemy zapisać w postaci
, to lewą stronę możemy zapisać w postaci
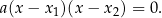
W przypadku samego rozwiązywania równania niewiele mądrego z tego wynika, ale w przypadku innych zadań (szczególnie z funkcją kwadratową) jest to bardzo ważne. W zasadzie o wzorach na pierwiastki powinno się myśleć nie jak o wzorach na rozwiązania równania kwadratowego, ale jak o wzorach pozwalających rozłożyć wyrażenie 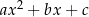 na iloczyn
na iloczyn 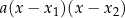 (nawet jak nie ma równania). Im szybciej nauczymy się tak myśleć, tym łatwiej będziemy rozwiązywać różne zadania z funkcją kwadratową.
(nawet jak nie ma równania). Im szybciej nauczymy się tak myśleć, tym łatwiej będziemy rozwiązywać różne zadania z funkcją kwadratową.
Spróbujmy uzasadnić, że dla dowolnej liczby całkowitej  liczba
liczba
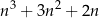
jest podzielna przez 3. Przekształcamy podane wyrażenie
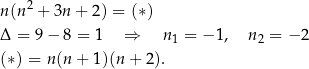
Otrzymaliśmy iloczyn trzech kolejnych liczb całkowitych – na pewno jedna z nich dzieli się przez 3.
Jeżeli 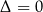 to rozkład jest ten sam, ale należy myśleć, że są dwa równe pierwiastki
to rozkład jest ten sam, ale należy myśleć, że są dwa równe pierwiastki
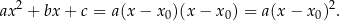
Uprośćmy wzór funkcji
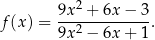
Licząc pierwiastki licznika i mianownika (z 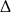 -y) mamy rozkład
-y) mamy rozkład
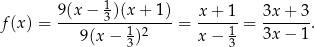
7Równania kwadratowe są blisko związane z równaniami z wartością bezwzględną. Związek ten pochodzi od równości:
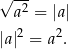
Rozwiążmy równanie 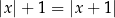 .
.
Obie strony są nieujemne, więc podnosimy równanie stronami do kwadratu.


