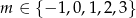/Szkoła średnia/Równania/Kwadratowe/Z parametrem

Zadanie nr 3473581

Dla jakich całkowitych wartości parametru 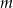m pierwiastkami równania 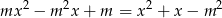mx 2 − m 2x + m = x2 + x − m 2 są liczby całkowite?

Wersja PDF

Rozwiązanie

Zapiszmy równanie w postaci

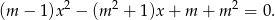
2 2 2 (m − 1)x − (m + 1 )x + m + m = 0.

Na początek sprawdźmy co się dzieje gdy równanie nie jest kwadratowe, czyli dla 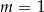m = 1 . Mamy wtedy równanie

−2x + 2 = 0 ⇒ x = 1.

Zatem jest OK.

Na razie zostawmy problem istnienia pierwiastków i zapiszmy wzory Viète’a dla tego równania.

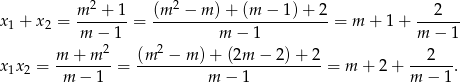
m 2 + 1 (m 2 − m )+ (m − 1) + 2 2 x 1 + x 2 =------- = ------------------------ = m + 1 + ------ m − 1 m − 1 m − 1 m--+-m-2 (m-2-−-m-)+-(2m--−-2)-+-2 --2--- x 1x2 = m − 1 = m − 1 = m + 2 + m − 1 .

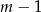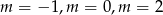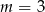Skoro i m i pierwiastki mają być całkowite, m − 1 musi dzielić 2. Czyli m − 1 jest równe -2,-1,1 lub 2. Daje to odpowiednio m = − 1,m = 0,m = 2 lub m = 3 . Daje to nam odpowiednio równania:

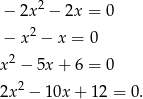
2 − 2x − 2x = 0 − x2 − x = 0 2 x − 5x + 6 = 0 2x 2 − 10x + 12 = 0.

Łatwo sprawdzić, że pierwiastki każdego z tych równań są całkowite.  
Odpowiedź: m ∈ {− 1,0,1 ,2 ,3}

Wersja PDF