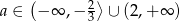/Szkoła średnia/Równania/Kwadratowe/Z parametrem

Zadanie nr 5017857

Dodaj do ulubionych
Dodaj do rozwiązanych

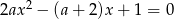Dla jakich wartości parametru a równanie 2 2ax − (a+ 2)x+ 1 = 0 ma dwa różne pierwiastki, których suma jest liczbą z przedziału ⟨− 1;1⟩ ?

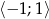Rozwiązanie

Sprawdźmy najpierw kiedy równanie ma dwa pierwiastki. Oczywiście musi być kwadratowe, czyli 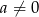a ⁄= 0 oraz

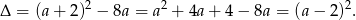
Δ = (a + 2)2 − 8a = a2 + 4a + 4 − 8a = (a− 2)2.

Widzimy, że równanie ma dwa różne pierwiastki dla 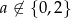a ⁄∈ {0,2} .

Na mocy wzorów Viète’a mamy

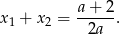
a-+-2- x1 + x2 = 2a .

Musimy więc rozwiązać nierówności

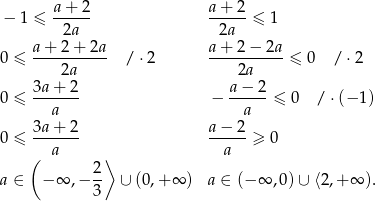
− 1 ≤ a+-2-- a+--2-≤ 1 2a 2a a+--2+--2a- a+--2−--2a- 0 ≤ 2a / ⋅2 2a ≤ 0 / ⋅2 3a+ 2 a− 2 0 ≤ ------- − ------≤ 0 / ⋅(− 1 ) a a 3a+--2- a−--2- 0 ≤ a a ≥ 0 ( 2⟩ a ∈ − ∞ ,− -- ∪ (0,+ ∞ ) a ∈ (−∞ ,0 )∪ ⟨2,+ ∞ ). 3

Uwzględniając jeszcze warunek 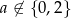a ⁄∈ {0,2} mamy

( 2 ⟩ a ∈ − ∞ ,− -- ∪ (2,+ ∞ ). 3

 
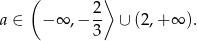
Odpowiedź: ( ⟩ a ∈ − ∞ ,− 23 ∪ (2,+ ∞ )

Wersja PDF