Zadanie nr 7564216
Wykaż, że jeśli funkcja kwadratowa 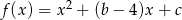 osiąga najmniejszą wartość dla argumentu
osiąga najmniejszą wartość dla argumentu  , to ma dwa rózne miejsca zerowe wtedy i tylko wtedy, gdy
, to ma dwa rózne miejsca zerowe wtedy i tylko wtedy, gdy 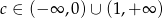 .
.
Rozwiązanie
Sposób I
Ze wzoru na współrzędną wierzchołka wiemy, że funkcja osiąga najmniejszą wartość w punkcie 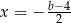 . Zatem
. Zatem
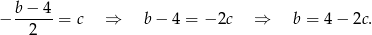
Mamay zatem równanie
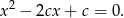
Musimy sprawdzić kiedy 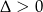 .
.
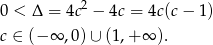
Sposób II
Jak poprzednio dochodzimy do równości:
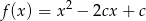
Skoro wiemy, że wierzchołek jest w punkcie  , wystarczy sprawdzić kiedy
, wystarczy sprawdzić kiedy 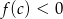 .
.