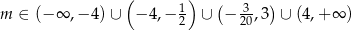Zadanie nr 7743378

Wyznacz wszystkie wartości parametru 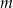, dla których równanie

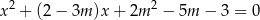
2 2 x + (2 − 3m )x + 2m − 5m − 3 = 0

ma dwa różne rozwiązania, których suma odwrotności jest mniejsza od 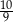109 .

Rozwiązanie

Sprawdźmy najpierw kiedy podane równanie ma dwa pierwiastki.

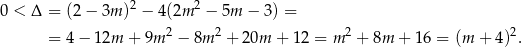
2 2 0 < Δ = (2 − 3m ) − 4(2m − 5m − 3 ) = = 4 − 12m + 9m 2 − 8m 2 + 2 0m + 1 2 = m 2 + 8m + 16 = (m + 4)2.

Musimy więc mieć 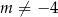m ⁄= − 4 . Przy tym założeniu możemy skorzystać ze wzorów Viète’a.

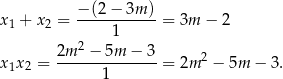
x + x = −-(2−--3m-) = 3m − 2 1 2 1 2m 2 − 5m − 3 x 1x2 = -------------- = 2m 2 − 5m − 3. 1

Pozostało rozwiązać nierówność

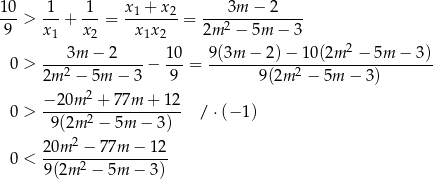
10 1 1 x 1 + x 2 3m − 2 -9-> x--+ x--= --x-x---= 2m-2-−-5m-−--3 1 2 1 2 ----3m-−-2---- 10- 9(3m--−-2)−--10(2m-2 −-5m-−--3) 0 > 2m 2 − 5m − 3 − 9 = 9(2m 2 − 5m − 3) 2 0 > −-20m---+-77m--+-12 / ⋅(− 1) 9(2m 2 − 5m − 3) 2 0 < 20m---−-77m--−-12- 9(2m 2 − 5m − 3)

Rozkładamy licznik i mianownik. Najpierw licznik.

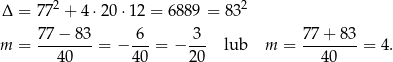
Δ = 772 + 4 ⋅20⋅ 12 = 6889 = 832 m = 77-−-83-= − -6-= − 3-- lub m = 77+--83-= 4. 40 40 20 40

Rozkładamy mianownik

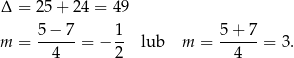
Δ = 25+ 24 = 49 5-−-7- 1- 5-+-7- m = 4 = − 2 lub m = 4 = 3.

Mamy więc do rozwiązania nierówność

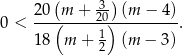
( ) 20--m-+--320--(m-−--4) 0 < ( 1) . 18 m + 2 (m − 3)

Nierówność ta jest równoważna nierówności wielomianowej

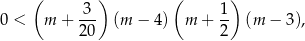
( ) ( ) 3-- 1- 0 < m + 20 (m − 4) m + 2 (m − 3),

której rozwiązaniem jest zbiór

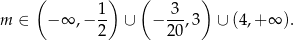
( 1 ) ( 3 ) m ∈ − ∞ ,− -- ∪ − --,3 ∪ (4,+ ∞ ). 2 20

Musimy jeszcze uwzględnić warunek 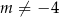m ⁄= − 4 . Rozwiązaniem jest więc zbiór

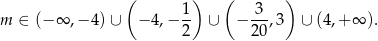
( ) ( ) m ∈ (− ∞ ,−4 )∪ − 4,− 1- ∪ − 3-,3 ∪ (4 ,+ ∞ ). 2 20

Odpowiedź: ( ) m ∈ (− ∞ ,−4 )∪ −4 ,− 1 ∪ (− 3-,3) ∪ (4,+ ∞ ) 2 20