Zadanie nr 7775983

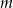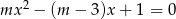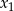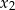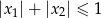Dla jakich wartości parametru równanie 2 mx − (m − 3)x+ 1 = 0 ma różne pierwiastki i x 2 spełniające warunek |x1| + |x2| ≤ 1 ?

Rozwiązanie

Sprawdźmy najpierw kiedy równanie ma dwa różne pierwiastki. Oczywiście musi być kwadratowe, czyli 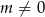m ⁄= 0 oraz

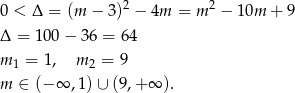
2 2 0 < Δ = (m − 3 ) − 4m = m − 10m + 9 Δ = 100− 36 = 64 m 1 = 1, m 2 = 9 m ∈ (− ∞ ,1 )∪ (9,+ ∞ ).

Ponieważ obie strony podanej nierówności są dodatnie, to podnosząc ją do kwadratu otrzymamy nierówność równoważną wyjściowej.

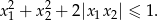
2 2 x1 + x2 + 2|x1x2| ≤ 1.

Skorzystamy teraz ze wzorów Viète’a

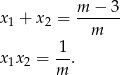
x1 + x2 = m--−-3 m -1 x1x2 = m .

Liczymy

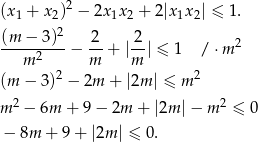
2 (x 1 + x 2) − 2x 1x2 + 2|x 1x2| ≤ 1. (m-−-3)2- -2 -2 2 m 2 − m + |m | ≤ 1 /⋅ m 2 2 (m − 3) − 2m + |2m | ≤ m m 2 − 6m + 9− 2m + |2m |− m2 ≤ 0 − 8m + 9+ |2m | ≤ 0.

Musimy teraz rozważyć dwa przypadki.

Jeżeli 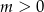m > 0 to

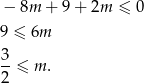
− 8m + 9+ 2m ≤ 0 9 ≤ 6m 3-≤ m . 2

Uzględniając warunek z 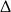-ą, mamy zatem m > 9 .

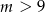Jeżeli 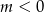m < 0 , to mamy

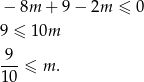
− 8m + 9− 2m ≤ 0 9 ≤ 10m -9-≤ m . 10

Ponieważ 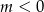m < 0 , nierówność ta jest sprzeczna.
Odpowiedź: m > 9