Zadanie nr 9003986
Wyznacz te wartości parametru 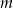 , dla których równanie
, dla których równanie 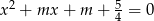 ma dwa różne pierwiastki nieujemne.
ma dwa różne pierwiastki nieujemne.
Rozwiązanie
Sprawdźmy najpierw kiedy podane równanie ma dwa różne pierwiastki. Liczymy
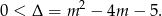
Rozwiązujemy tę nierówność kwadratową, 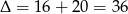 ,
, 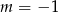 lub
lub 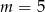 . Zatem
. Zatem 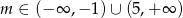 .
.
Oba pierwiastki są nieujemne, jeżeli ich suma i iloczyn są nieujemne. Na mocy wzorów Viète’a, mamy
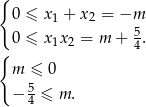
Uwzględniając nierówność pochodzącą od 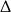 –y, mamy
–y, mamy 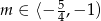
Odpowiedź: