/Szkoła średnia/Równania/Kwadratowe/Z parametrem

Zadanie nr 9117736

Dodaj do ulubionych
Dodaj do rozwiązanych

Określ liczbę pierwiastków równania 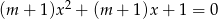2 (m + 1 )x + (m + 1)x + 1 = 0 w zależności od wartości parametru 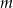m , a następnie naszkicuj wykres funkcji:

( |{ x1 + x2 gdy dane równanie ma dwa pierwiastki x1 i x2, f(m ) = |( 2x0 gdy dane równanie ma jeden pierwiastek x 0, 3− m gdy dane równanie nie ma pierwiastków .

Rozwiązanie

Jeżeli równanie jest liniowe, czyli 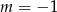m = − 1 , to mamy równanie 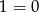1 = 0 , które jest sprzeczne.

Jeżeli równanie jest kwadratowe, to o ilości jego pierwiastków decyduje znak 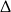Δ -y.

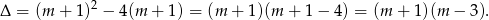
Δ = (m + 1)2 − 4(m + 1) = (m + 1 )(m + 1 − 4) = (m + 1)(m − 3).

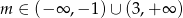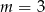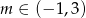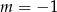Zatem równanie ma dwa pierwiastki dla m ∈ (− ∞ ,− 1)∪ (3,+ ∞ ) , ma jeden pierwiastek dla m = 3 i nie ma pierwiastków dla m ∈ (− 1,3) oraz m = −1 (to sprawdziliśmy na początku). Ponadto na mocy wzorów Viète’a mamy

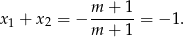
m + 1 x 1 + x 2 = −------= − 1. m + 1

Łatwo sprawdzić, że wzór ten działa również dla 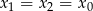x = x = x 1 2 0 , czyli w sytuacji gdy Δ = 0 .

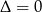Określona w treści zadania funkcja 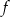f ma więc wzór

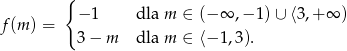
{ − 1 dla m ∈ (− ∞ ,− 1) ∪ ⟨3,+ ∞ ) f(m ) = 3− m dla m ∈ ⟨− 1,3).

Bez trudu szkicujemy jej wykres.

PIC

 
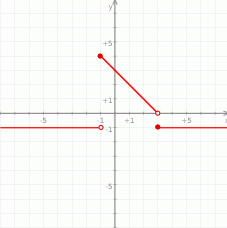
Odpowiedź: { −1 dla m ∈ (− ∞ ,− 1)∪ ⟨3,+ ∞ ) f(m ) = 3− m dla m ∈ ⟨− 1,3).

Wersja PDF