/Szkoła średnia/Równania/Kwadratowe/Z parametrem

Zadanie nr 9120517

Dodaj do ulubionych
Dodaj do rozwiązanych

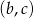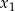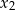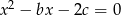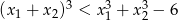W prostokątnym układzie współrzędnych narysuj zbiór tych wszystkich punktów o współrzędnych (b,c) , dla których różne pierwiastki x1 i x2 równania x 2 − bx − 2c = 0 spełniają warunek (x1 + x2)3 < x31 + x32 − 6 .

PIC

Rozwiązanie

Korzystamy ze wzorów Viéte’a

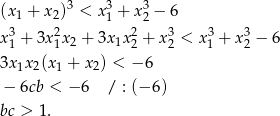
3 3 3 (x1 + x2) < x1 + x2 − 6 x31 + 3x21x2 + 3x 1x22 + x32 < x31 + x32 − 6 3x1x2(x 1 + x 2) < − 6 − 6cb < − 6 / : (− 6) bc > 1.

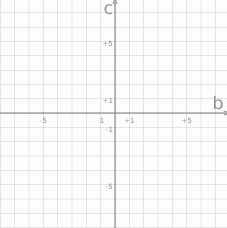
Punkty spełniające tę nierównośc, to punkty leżące ’wewnątrz’ gałęzi hiperboli 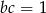bc = 1 .

PIC

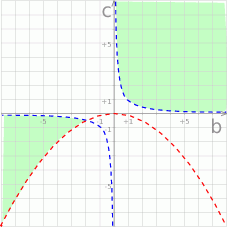
Ponieważ równanie ma mieć dwa pierwiastki, to musi być jeszcze spełnione

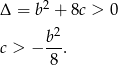
Δ = b2 + 8c > 0 2 c > − b--. 8

Musimy zatem ograniczyć się do punktów leżących powyżej paraboli 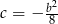c = − b2- 8 .

Wersja PDF