/Szkoła średnia/Równania/Kwadratowe/Z parametrem

Zadanie nr 9298152

Dodaj do ulubionych
Dodaj do rozwiązanych

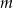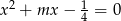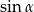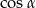Dla jakich wartości parametru m pierwiastkami równania 2 1 x + mx − 4 = 0 są liczby liczby sin α i cosα dla pewnego α ∈ R ?

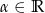Rozwiązanie

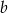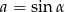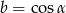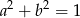Dwie liczby rzeczywiste a i b są postaci a = sin α i b = cosα dla pewnego α , wtedy i tylko wtedy gdy a2 + b2 = 1 (jedynka trygonometryczna). Aby sprawdzić, kiedy pierwiastki podanego równania spełniają taki warunek, korzystamy ze wzorów Viète’a.

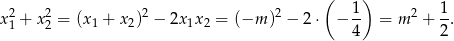
( ) 2 2 2 2 1- 2 1- x1 + x2 = (x 1 + x 2) − 2x 1x2 = (−m ) − 2 ⋅ − 4 = m + 2.

Mamy zatem równanie

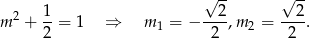
√ -- √ -- m 2 + 1-= 1 ⇒ m = − --2,m = --2-. 2 1 2 2 2

To, co koniecznie trzeba jeszcze sprawdzić, to czy dla wyliczonych wartości 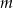m równanie ma w ogóle pierwiastki, tzn. czy 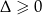Δ ≥ 0 . Dla obu wartości 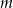m mamy Δ = 3 2 .  
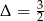Odpowiedź: 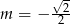√ - m = − -22 lub √- m = -22-

Wersja PDF