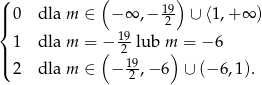Zadanie nr 9383246

Naszkicuj wykres funkcji, która każdej liczbie rzeczywistej 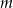przyporządkowuje liczbę pierwiastków równania

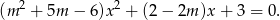
(m 2 + 5m − 6)x2 + (2 − 2m )x + 3 = 0 .

Rozwiązanie

Sprawdźmy najpierw co się dzieje, gdy równanie nie jest kwadratowe.

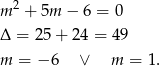
2 m + 5m − 6 = 0 Δ = 25 + 24 = 49 m = − 6 ∨ m = 1.

Mamy wtedy odpowiednio

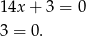
14x + 3 = 0 3 = 0 .

Zatem dla 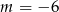m = − 6 mamy jedno rozwiązanie, a dla 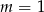m = 1 równanie nie ma rozwiązań.

Jeżeli równanie jest kwadratowe, to decydujący jest znak 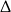-y.

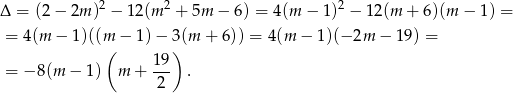
Δ = (2− 2m )2 − 12 (m2 + 5m − 6) = 4(m − 1)2 − 12(m + 6)(m − 1 ) = = 4(m − 1)((m − 1 )− 3 (m + 6)) = 4 (m − 1)(− 2m − 19) = ( 19) = − 8(m − 1) m + --- . 2

Widać więc, że

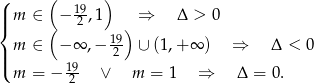
( ( 19 ) ||{ m ∈ ( − 2 ,1 ) ⇒ Δ > 0 19- || m ∈ −∞ ,− 2 ∪ (1 ,+∞ ) ⇒ Δ < 0 ( m = − 19- ∨ m = 1 ⇒ Δ = 0. 2

Zatem ilość rozwiązań równania wyraża się wzorem

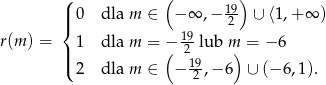
( ) (| 19 |{ 0 dla m ∈ − ∞ ,− 2 ∪ ⟨1,+ ∞ ) r(m ) = 1 dla m = − 19 lub m = − 6 ||( ( 219 ) 2 dla m ∈ − -2 ,− 6 ∪ (− 6,1).

Teraz bez trudu szkicujemy żądany wykres.

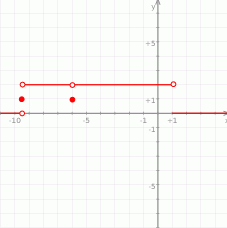
Odpowiedź: ( ( ) || 0 dla m ∈ − ∞ ,− 129 ∪ ⟨1,+ ∞ ) { 19 | 1 dla m = (− 2-lub m) = − 6 |( 2 dla m ∈ − 19,− 6 ∪ (− 6,1). 2