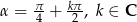/Szkoła średnia/Równania/Kwadratowe/Z parametrem

Zadanie nr 9571692

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru α suma kwadratów różnych pierwiastków równania

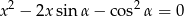
x 2 − 2x sinα − c os2α = 0

jest równa 3?

Rozwiązanie

Sprawdźmy najpierw kiedy równanie ma dwa różne pierwiastki.

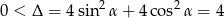
2 2 0 < Δ = 4sin α+ 4cos α = 4

Nierówność ta jest zawsze spełniona, więc równanie ma zawsze dwa pierwiastki 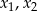x1,x 2 .

Na mocy wzorów Viète’a mamy

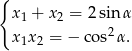
{ x1 + x2 = 2sin α 2 x1x2 = − co s α.

Musimy rozwiązać równanie

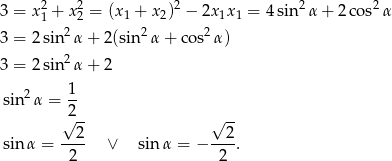
2 2 2 2 2 3 = x1 + x2 = (x1 + x2) − 2x1x1 = 4sin α + 2 cos α 3 = 2sin2α + 2 (sin2 α + cos2α ) 3 = 2sin2α + 2 1 sin 2α = -- √2-- √ -- --2- --2- sin α = 2 ∨ sinα = − 2 .

Szkicujemy teraz sinusa.

PIC

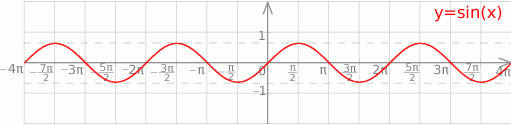
Z wykresu odczytujemy rozwiązanie:

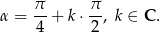
π π α = --+ k ⋅--, k ∈ C. 4 2

 
Odpowiedź: π- kπ- α = 4 + 2 , k ∈ C

Wersja PDF