/Szkoła średnia/Równania/Kwadratowe/Z parametrem

Zadanie nr 9638346

Dodaj do ulubionych
Dodaj do rozwiązanych

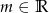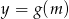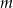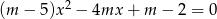Zbadaj liczbę rozwiązań równania ze względu na wartość parametru m ∈ R . Napisz wzór i narysuj wykres funkcji y = g(m ) , która każdej wartości parametru m przyporządkowuje liczbę rozwiązań równania (m − 5)x2 − 4mx + m − 2 = 0 .

Rozwiązanie

Sprawdźmy najpierw co się dzieje gdy równanie nie jest kwadratowe, czyli dla 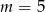m = 5 . Mamy wtedy równanie

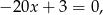
− 20x + 3 = 0 ,

które ma dokładnie jedno rozwiązanie.

Jeżeli równanie jest kwadratowe, to liczymy 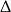Δ -ę.

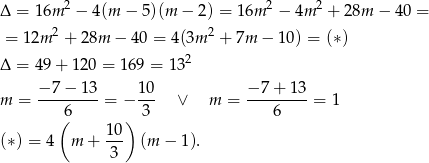
Δ = 16m 2 − 4(m − 5)(m − 2) = 16m 2 − 4m 2 + 28m − 40 = 2 2 = 12m + 28m − 40 = 4(3m + 7m − 10) = (∗) Δ = 49 + 1 20 = 169 = 132 m = −-7−--13-= − 1-0 ∨ m = −-7-+-13-= 1 (6 ) 3 6 10 (∗) = 4 m + -3- (m − 1).

Zatem ilość rozwiązań równania wyraża się wzorem

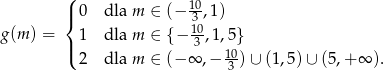
( |{ 0 dla m ∈ (− 103 ,1) g(m ) = 1 dla m ∈ { − 10,1,5} |( 3 10 2 dla m ∈ (− ∞ ,− -3 ) ∪ (1,5)∪ (5 ,+∞ ).

Teraz bez trudu szkicujemy wykres.

PIC

 
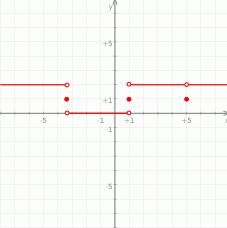
Odpowiedź: ( |{ 0 dla m ∈ (− 130,1) g(m ) = 1 dla m ∈ {− 10,1,5} |( 3 2 dla m ∈ (−∞ ,− 103-)∪ (1,5) ∪ (5,+ ∞ ).

Wersja PDF