/Szkoła średnia/Równania/Kwadratowe/Z parametrem

Zadanie nr 9641391

Dodaj do ulubionych
Dodaj do rozwiązanych

Dane są niezerowe liczby wymierne 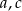a,c takie, że funkcja 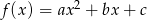2 f(x) = ax + bx+ c ma miejsce zerowe będące liczbą wymierną. Wykaż, że 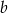b jest liczbą wymierną.

Rozwiązanie

Niech 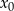x0 będzie wymiernym miejscem zerowym funkcji 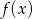f(x) , tzn.

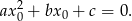
2 ax0 + bx0 + c = 0.

Zauważmy, że 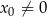x0 ⁄= 0 , bo z założenia 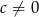c ⁄= 0 . Z powyższej równości możemy wyliczyć b .

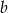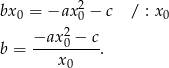
2 bx 0 = −ax 0 − c / : x 0 −ax 2 − c b = ----0----. x0

Wszystkie liczby po prawej stronie są wymierne, więc 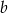b też jest liczbą wymierną.

Wersja PDF