Ramiona trapezu są średnicami dwóch okręgów. Wykaż, że jeśli okręgi te są styczne zewnętrznie, to w trapez ten można wpisać okrąg.
Zaczynamy od rysunku.
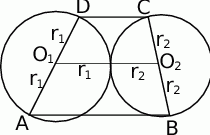
Ponieważ punkt styczności dwóch stycznych okręgów leży na prostej łączącej ich środki, to odcinek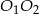 
jest odcinkiem łączącym środki ramion trapezu i ma długość 
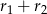. Łątwo wykazać, że w dowolnym trapezie długość tego odcinka jest średnią arytmetyczną równoległych podstaw. Zatem
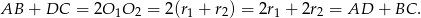
Równość ta jest warunkiem wystarczającym do tego, żeby w czworokąt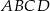 
można było wpisać okrąg.
Informacje
Zadania
Losowe zadanie
