/Konkursy/Zadania/Geometria/Planimetria/Trapez/Różne

Zadanie nr 9771471

Dodaj do ulubionych
Dodaj do rozwiązanych

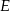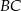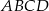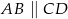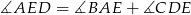Punkt E leży na ramieniu BC trapezu ABCD , w którym AB ∥ CD . Udowodnij, że ∡AED = ∡BAE + ∡CDE .

Rozwiązanie

Zaczynamy oczywiście od rysunku.

Sposób I

PIC

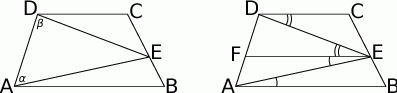
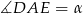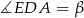Jeżeli oznaczymy ∡DAE = α i ∡EDA = β , to z trójkąta 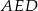AED mamy

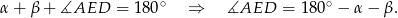
α + β + ∡AED = 180 ∘ ⇒ ∡AED = 180∘ − α − β .

Z drugiej strony mamy

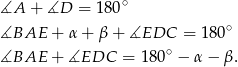
∡A + ∡D = 180∘ ∘ ∡BAE + α + β + ∡EDC = 180 ∡BAE + ∡EDC = 180∘ − α − β .

Widać więc, że

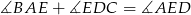
∡BAE + ∡EDC = ∡AED

Sposób II

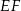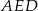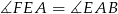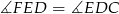Jeżeli dorysujemy odcinek EF równoległy do podstaw trapezu, to widać, że kąt AED został podzielony na dwa kąty ∡F EA = ∡EAB i ∡F ED = ∡EDC , co dowodzi tezy.

Wersja PDF