/Konkursy/Zadania/Geometria/Planimetria/Kwadrat

Zadanie nr 6412799

Dodaj do ulubionych
Dodaj do rozwiązanych

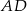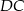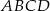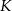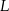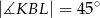Na bokach AD i DC kwadratu ABCD o polu 1 wybrano punkty K i L w ten sposób, że |∡KBL | = 45∘ .

PIC

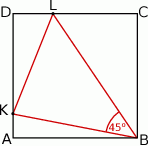
Oblicz odległość punktu B od prostej KL .

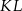Rozwiązanie

Sposób I

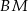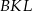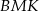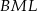Jeżeli dorysujemy wysokość BM trójkąta BKL , to trudno oprzeć się wrażeniu, że trójkąty BMK i BML są przystające do trójkątów 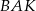BAK i BCL .

PIC

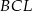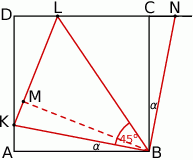
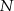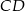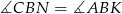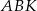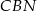Spróbujmy uzasadnić, że rzeczywiście tak jest. Niech N będzie takim punktem prostej CD , że ∡CBN = ∡ABK . Trójkąty prostokątne ABK i CBN mają równe kąty oraz 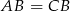AB = CB , więc są przystające. W szczególności 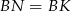BN = BK . Ponadto

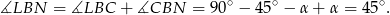
∘ ∘ ∘ ∡LBN = ∡LBC + ∡CBN = 90 − 45 − α + α = 45 .

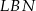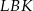To oznacza, że trójkąty LBN i LBK mają takie same kąty przy wierzchołku 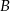B oraz boki przylegające do tych kątów są tej samej długości. Trójkąty te są więc przystające. W takim razie odpowiadające sobie wysokości tych trójkątów też są równe, więc

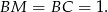
BM = BC = 1.

Sposób II

Tym razem użyjemy trygonometrii. Spróbujemy najpierw obliczyć boki trójkąta 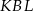KBL w zależności od 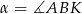α = ∡ABK . Mamy więc

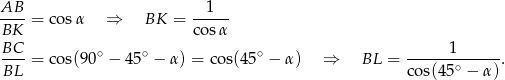
AB 1 BK--= co sα ⇒ BK = cosα- BC--= co s(90∘ − 45∘ − α) = cos(4 5∘ − α) ⇒ BL = ------1------. BL cos(4 5∘ − α)

Długość odcinka 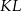KL obliczamy z twierdzenia cosinusów.

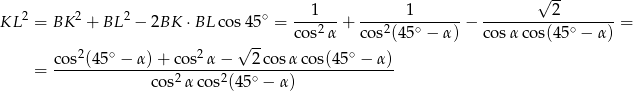
√ -- 1 1 2 KL 2 = BK 2 + BL 2 − 2BK ⋅BL cos45 ∘ = ---2--+ ---2----∘-----− ------------∘----- = √ -- cos α cos (45 − α ) cosα cos(45 − α ) cos2(4 5∘ − α )+ cos2α − 2 cosα cos(45∘ − α ) = -----------------2-----2---∘------------------- cos α cos (45 − α)

Zauważmy teraz, że

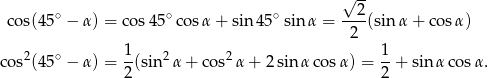
√ -- cos(45∘ − α) = co s45∘ cosα + sin 45∘sin α = --2-(sin α + cos α) 2 2 ∘ 1- 2 2 1- cos (45 − α) = 2(sin α + co s α + 2sin αco sα) = 2 + sin α cosα .

Stąd

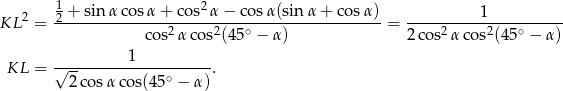
1 + sin αco sα + cos2 α− cosα(sin α + cosα ) 1 KL 2 = 2-------------------------------------------- = ---------------------- cos2α cos2(45∘ − α) 2 cos2α cos2(45 ∘ − α ) 1 KL = √---------------∘-----. 2 cosα cos(45 − α )

Odcinek 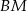BM jest wysokością w trójkącie 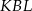KBL , więc porównując dwa wzory na jego pole mamy

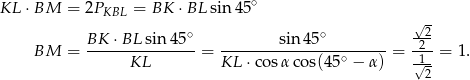
KL ⋅BM = 2PKBL = BK ⋅BL sin 45∘ √ - BK-⋅BL--sin-45∘- --------sin45-∘-------- -22 BM = KL = KL ⋅ cosα cos(45∘ − α) = √1- = 1 . 2

 
Odpowiedź: 1

Wersja PDF