Zadanie nr 1137845
Rzucamy trzy razy monetą, a następnie rzucamy tyle razy kostką, ile orłów otrzymaliśmy w rzutach monetami. Oblicz prawdopodobieństwo tego, że suma oczek otrzymanych w rzutach kostką jest dwa razy większa od liczby orłów otrzymanych w rzutach monetą jeżeli wiadomo, że w rzutach monetą otrzymaliśmy przynajmniej jednego orła.
Rozwiązanie
Wszystkich wyników trzykrotnego rzutu monetą jest
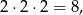
ale wiemy, że wylosowano co najmniej jednego orła, więc wyniku 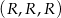 nie bierzemy pod uwagę. Możliwe wyniki rzutu monetą dzielimy na trzy grupy w zależności od liczby wylosowanych orłów:
nie bierzemy pod uwagę. Możliwe wyniki rzutu monetą dzielimy na trzy grupy w zależności od liczby wylosowanych orłów:
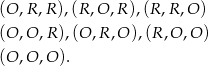
Prawdopodobieństwa otrzymania 1, 2 lub 3 orłów są więc odpowiednio równe 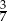 ,
, 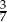 i
i 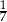 .
.
Jeżeli w rzutach monetą otrzymaliśmy jednego orła, to potem rzucamy jedną kostką i prawdopodobieństwo otrzymania na niej 2 oczek jest równe  .
.
Jeżeli w rzutach monetą otrzymaliśmy dwa orły, to potem rzucamy dwa razy kostką i prawdopodobieństwo otrzymania na nich sumy oczek równej 4 jest równe
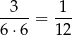
(bo są 3 zdarzenia sprzyjające: 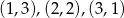 ).
).
Zajmijmy się ostatnią sytuacją, gdy w rzucie monetą otrzymaliśmy 3 orły. Wtedy rzucamy 3 razy kostką i interesują nas zdarzenia, w których suma oczek jest równa 6. Jest 10 takich zdarzeń
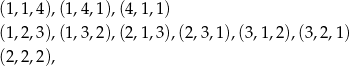
więc prawdopodobieństwo otrzymania sumy oczek równej 6 jest równe
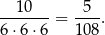
Teraz rysujemy drzewko opisujące możliwe przebiegi losowania.
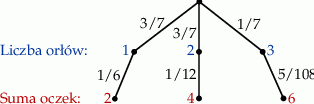
Odczytujemy z drzewka interesujące nas prawdopodobieństwo.
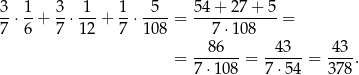
Odpowiedź: