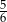/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite

Zadanie nr 2703883

Dodaj do ulubionych
Dodaj do rozwiązanych

Wśród 200 uczniów pewnego krakowskiego gimnazjum przeprowadzono ankietę dotyczącą planów wakacyjnych. Wyniki ankiety przedstawiono w tabeli.

Klasa  Liczba uczniów Liczba uczniów,
którzy nie wyjadą
na wakacje 		Liczba uczniów,
którzy wyjadą
z rodzicami 		Liczba uczniów,
którzy wyjadą
na kolonie
Pierwsza 50 8 36 12
Druga 80 16 48 24
Trzecia 70 12 40 24

Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrana osoba, spośród ankietowanych, wyjedzie na wakacje, jeśli wiadomo, że ta osoba nie jest uczniem drugiej klasy.

Rozwiązanie

Sposób I

Jeżeli oznaczymy przez 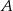A zdarzenie polegające na tym, że losowo wybrany uczeń wyjedzie na wakacje, a przez 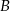B zdarzenie polegające na tym, że losowo wybrana osoba jest uczniem pierwszej lub trzeciej klasy, to musimy obliczyć

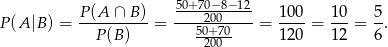
P (A ∩ B ) 50+-70−-8−12 100 10 5 P (A |B ) = ----------= ---5200+070--- = ----= ---= -. P (B) 200 120 12 6

Sposób II

Ponieważ interesują nas tylko uczniowie pierwszej i trzeciej klasy, pomijamy zupełnie drugi wiersz tabeli i interesujące nas prawdopodobieństwo jest równe

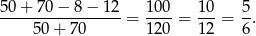
50+--70−--8−--12-= 100-= 10-= 5. 50 + 70 120 12 6

 
Odpowiedź: 56

Wersja PDF